
題目列表(包括答案和解析)
平面直角坐標系內的向量都可以用一有序實數對唯一表示,這使我們想到可以用向量作為解析幾何的研究工具.如圖,設直線
l的傾斜角為α(α≠90°).在l上任取兩個不同的點 ,
, ,不妨設向量
,不妨設向量 的方向是向上的,那么向量
的方向是向上的,那么向量 的坐標是(
的坐標是( ).過原點作向量
).過原點作向量 ,則點P的坐標是(
,則點P的坐標是( ),而且直線OP的傾斜角也是α.根據正切函數的定義得
),而且直線OP的傾斜角也是α.根據正切函數的定義得
 ,
,
這就是《數學
2》中已經得到的斜率公式.上述推導過程比《數學2》中的推導簡捷.你能用向量作為工具討論一下直線的有關問題嗎?例如:(1)
過點 ,平行于向量
,平行于向量 的直線方程;
的直線方程;
(2)
向量(A,B)與直線 的關系;
的關系;
(3)
設直線 和
和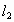 的方程分別是
的方程分別是
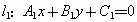

那么,
 ∥
∥ ,
, 的條件各是什么?如果它們相交,如何得到它們的夾角公式?
的條件各是什么?如果它們相交,如何得到它們的夾角公式?
(4)
點 到直線
到直線 的距離公式如何推導?
的距離公式如何推導?

(本小題滿分14分)
已知函數 ,當
,當 時,
時, 取得極
取得極 小值
小值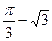 .
.
(1)求 ,
, 的值;
的值;
(2)設直線 ,曲線
,曲線 .若直線
.若直線
 與曲線
與曲線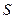 同時滿足下列兩個條件:
同時滿足下列兩個條件:
①直線 與曲線
與曲線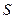 相切且至少有兩個
相切且至少有兩個 切點;
切點;
②對任意 都有
都有 .則稱直線
.則稱直線 為曲線
為曲線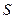 的“上夾線”.
的“上夾線”.
試證明:直線 是曲線
是曲線 的“上夾線”.
的“上夾線”.
(3)記 ,設
,設 是方程
是方程 的實數
的實數 根,若對于
根,若對于 定義域中任意的
定義域中任意的 、
、 ,當
,當 ,且
,且 時,問是否存在一個最小的正整數
時,問是否存在一個最小的正整數 ,使得
,使得 恒成立,若存在請求出
恒成立,若存在請求出 的值;若不存在請說明理由.
的值;若不存在請說明理由.
(本小題滿分14分)
已知函數 ,當
,當 時,
時, 取得極小值
取得極小值 .
.
(1)求 ,
, 的值;
的值;
(2)設直線 ,曲線
,曲線 .若直線
.若直線 與曲線
與曲線 同時滿足下列兩個條件:
同時滿足下列兩個條件:
①直線 與曲線
與曲線 相切且至少有兩個切點;
相切且至少有兩個切點;
②對任意 都有
都有 .則稱直線
.則稱直線 為曲線
為曲線 的“上夾線”.
的“上夾線”.
試證明:直線 是曲線
是曲線 的“上夾線”.
的“上夾線”.
(3)記 ,設
,設 是方程
是方程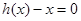 的實數根,若對于
的實數根,若對于 定義域中任意的
定義域中任意的 、
、 ,當
,當 ,且
,且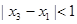 時,問是否存在一個最小的正整數
時,問是否存在一個最小的正整數 ,使得
,使得 恒成立,若存在請求出
恒成立,若存在請求出 的值;若不存在請說明理由.
的值;若不存在請說明理由.
(本小題滿分14分)
已知函數![]() ,當
,當![]() 時,
時,![]() 取得極小值
取得極小值![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)設直線![]() ,曲線
,曲線![]() .若直線
.若直線![]() 與曲線
與曲線![]() 同時滿足下列兩個條件:
同時滿足下列兩個條件:
①直線![]() 與曲線
與曲線![]() 相切且至少有兩個切點;
相切且至少有兩個切點;
②對任意![]() 都有
都有![]() .則稱直線
.則稱直線![]() 為曲線
為曲線![]() 的“上夾線”.
的“上夾線”.
試證明:直線![]() 是曲線
是曲線![]() 的“上夾線”.
的“上夾線”.
(3)記![]() ,設
,設![]() 是方程
是方程![]() 的實數根,若對于
的實數根,若對于![]() 定義域中任意的
定義域中任意的![]() 、
、![]() ,當
,當![]() ,且
,且![]() 時,問是否存在一個最小的正整數
時,問是否存在一個最小的正整數![]() ,使得
,使得![]() 恒成立,若存在請求出
恒成立,若存在請求出![]() 的值;若不存在請說明理由.
的值;若不存在請說明理由.
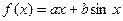 ,當
,當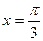 時,
時,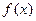 取得極
取得極 小值
小值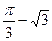 .
.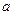 ,
,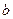 的值;
的值;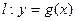 ,曲線
,曲線 .若直線
.若直線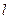
 與曲線
與曲線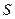 同時滿足下列兩個條件:
同時滿足下列兩個條件: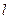 與曲線
與曲線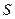 相切且至少有兩個
相切且至少有兩個 切點;
切點; 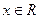 都有
都有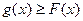 .則稱直線
.則稱直線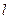 為曲線
為曲線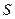 的“上夾線”.
的“上夾線”.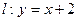 是曲線
是曲線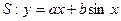 的“上夾線”.
的“上夾線”.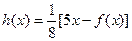 ,設
,設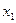 是方程
是方程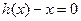 的實數
的實數 根,若對于
根,若對于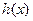 定義域中任意的
定義域中任意的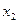 、
、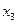 ,當
,當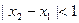 ,且
,且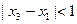 時,問是否存在一個最小的正整數
時,問是否存在一個最小的正整數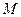 ,使得
,使得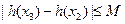 恒成立,若存在請求出
恒成立,若存在請求出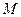 的值;若不存在請說明理由.
的值;若不存在請說明理由.一、選擇題:
1―5:BABDD 6―10:BABDC 11―12:AC
二、填空題:
13、1 14、 15、
15、 16、①③④
16、①③④
三、解答題:
17、解:(Ⅰ)
 ……………………(2分)
……………………(2分)
即 即
即
 ………………………………………………………………(4分)
………………………………………………………………(4分)
由于 ,故
,故 …………………………………………………(6分)
…………………………………………………(6分)
(Ⅱ)由 知
知 ,
,
 …………………………………………………………(8分)
…………………………………………………………(8分)
 …………(10分)
…………(10分)

當且僅當 ,即
,即 時,
時, 取得最大值
取得最大值 .
.
所以 的最大值為
的最大值為 ,此時
,此時 為等腰三角形.
為等腰三角形.
18、解析:(1)抽取的4根鋼管中恰有2根長度相同的概率為:
 ……………………………………………………………………(3分)
……………………………………………………………………(3分)
(2)新焊接成鋼管的長度的可能值有7種,最短的可能值為5m,最長的可能值為11m.
當 =5m與
=5m與 =11m時的概率為
=11m時的概率為 ;
;
當 =6m與
=6m與 =10m時的概率為
=10m時的概率為 ;tesoon
;tesoon
當 =7m與
=7m與 =9m時的概率為
=9m時的概率為 ;
;
當 =8m時的概率為
=8m時的概率為 .…………………………………………(9分)
.…………………………………………(9分)
 的分布列為:
的分布列為:

5
6
7
8
9
10
11








 …………………………(12分)
…………………………(12分)
19、(1)圓 ,當
,當 時,點
時,點 在圓上,故當且僅當直線
在圓上,故當且僅當直線 過圓心C時滿足
過圓心C時滿足 .
.
 圓心坐標為(1,1),
圓心坐標為(1,1), …………………………………………………………(3分)
…………………………………………………………(3分)
(2)由 ,消去
,消去 可得
可得 .
.
 得
得 ………………①
………………①
設 ,則
,則 ……………………………………(5分)
……………………………………(5分)

 ,即
,即 =0.
=0.
又 ,
, ,即
,即 .
.
 .
.
故 …………………………………………………………………………(9分)
…………………………………………………………………………(9分)
又 (當且僅當
(當且僅當 時取=)
時取=)
 即
即 ………………②
………………②
由①②知,
 直線
直線 的傾斜角取值范圍為:
的傾斜角取值范圍為: …………………………………………………(12分)
…………………………………………………(12分)
20、解:(1)設 ,
,
( )
) 在[-1,1]上是增函數………………………………………(3分)
在[-1,1]上是增函數………………………………………(3分)
(2) ,解得:
,解得: …………………………(7分)
…………………………(7分)
(3)對所有 恒成立,等價于
恒成立,等價于 的最大值不大于
的最大值不大于 .
.
又 在[-1,1]上是增函數,
在[-1,1]上是增函數, 在[-1,1]上的最大值為
在[-1,1]上的最大值為
即 ,得
,得 ,
,
設 ,是關于
,是關于 的一次函數,要使
的一次函數,要使 恒成立,
恒成立,
只需 即可,解得:
即可,解得: 或
或 或
或 .
.
21、解析:(1)設
 在
在 處有極值,
處有極值, 即
即
 在點(0,-3)處的切線平行于
在點(0,-3)處的切線平行于 即
即
故 …………………………………………………………………(4分)
…………………………………………………………………(4分)
(2)設
又 時,
時, (遞減)
(遞減)
 時,
時, (遞增)
(遞增)
 曲線
曲線 上任意兩點的連線的斜率恒大于
上任意兩點的連線的斜率恒大于 .
.
解不等式 得
得 .
.
 或
或 …………………………………………………………(8分)
…………………………………………………………(8分)
(3)設 ,則
,則 ,
, 時
時 為[0,1]上的增函數
為[0,1]上的增函數
 的值域是[-4.
的值域是[-4.  ].…………………………(12分)
].…………………………(12分)
22、解析:(1)圓 與
與 彼此外切,令
彼此外切,令 為圓
為圓 的半徑,
的半徑,
 即
即 ,
,
兩邊平方并化簡得 ,
,
由題意得,圓 的半徑
的半徑 ,
,
即 ……………………………………………………………………(5分)
……………………………………………………………………(5分)
 數列
數列 是以
是以 為首項,以2為公差的等差數列,
為首項,以2為公差的等差數列,
所以 即
即 .………………………………………………(8分)
.………………………………………………(8分)
(2) ,……………………………………………………(10分)
,……………………………………………………(10分)
因為
 …………………………………………………(12分)
…………………………………………………(12分)


所以 ………………………………………………………………………………(14分)
………………………………………………………………………………(14分)
 天星教育網(www.tesoon.com) 版權所有
天星教育網(www.tesoon.com) 版權所有
天星教育網(www.tesoon.com) 版權所有
天星教育網(www.tesoon.com) 版權所有