
題目列表(包括答案和解析)
A.2 B.![]() C.1 D.
C.1 D.![]()
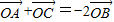 ,則△AOB與△AOC的面積之比為 .
,則△AOB與△AOC的面積之比為 .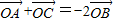 ,則△AOB與△AOC的面積之比為 .
,則△AOB與△AOC的面積之比為 .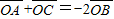 ,則△AOB與△AOC的面積之比為( )
,則△AOB與△AOC的面積之比為( )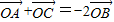 ,則△AOB與△AOC的面積之比為 .
,則△AOB與△AOC的面積之比為 .一、選擇題:
1―5:BABDD 6―10:BABDC 11―12:AC
二、填空題:
13、1 14、中學(xué)高三二診模擬數(shù)學(xué)理.files/image280.gif) 15、
15、中學(xué)高三二診模擬數(shù)學(xué)理.files/image282.gif) 16、①③④
16、①③④
三、解答題:
17、解:(Ⅰ)中學(xué)高三二診模擬數(shù)學(xué)理.files/image284.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image286.gif) ……………………(2分)
……………………(2分)
即中學(xué)高三二診模擬數(shù)學(xué)理.files/image288.gif) 即
即中學(xué)高三二診模擬數(shù)學(xué)理.files/image290.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image292.gif) ………………………………………………………………(4分)
………………………………………………………………(4分)
由于中學(xué)高三二診模擬數(shù)學(xué)理.files/image294.gif) ,故
,故中學(xué)高三二診模擬數(shù)學(xué)理.files/image296.gif) …………………………………………………(6分)
…………………………………………………(6分)
(Ⅱ)由中學(xué)高三二診模擬數(shù)學(xué)理.files/image298.gif) 知
知中學(xué)高三二診模擬數(shù)學(xué)理.files/image300.gif) ,
,
中學(xué)高三二診模擬數(shù)學(xué)理.files/image302.gif) …………………………………………………………(8分)
…………………………………………………………(8分)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image304.gif) …………(10分)
…………(10分)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image306.gif)
當(dāng)且僅當(dāng)中學(xué)高三二診模擬數(shù)學(xué)理.files/image308.gif) ,即
,即中學(xué)高三二診模擬數(shù)學(xué)理.files/image310.gif) 時(shí),
時(shí),中學(xué)高三二診模擬數(shù)學(xué)理.files/image312.gif) 取得最大值
取得最大值中學(xué)高三二診模擬數(shù)學(xué)理.files/image314.gif) .
.
所以中學(xué)高三二診模擬數(shù)學(xué)理.files/image189.gif) 的最大值為
的最大值為中學(xué)高三二診模擬數(shù)學(xué)理.files/image317.gif) ,此時(shí)
,此時(shí)中學(xué)高三二診模擬數(shù)學(xué)理.files/image079.gif) 為等腰三角形.
為等腰三角形.
18、解析:(1)抽取的4根鋼管中恰有2根長(zhǎng)度相同的概率為:
中學(xué)高三二診模擬數(shù)學(xué)理.files/image320.gif) ……………………………………………………………………(3分)
……………………………………………………………………(3分)
(2)新焊接成鋼管的長(zhǎng)度的可能值有7種,最短的可能值為5m,最長(zhǎng)的可能值為11m.
當(dāng)中學(xué)高三二診模擬數(shù)學(xué)理.files/image194.gif) =5m與
=5m與中學(xué)高三二診模擬數(shù)學(xué)理.files/image194.gif) =11m時(shí)的概率為
=11m時(shí)的概率為中學(xué)高三二診模擬數(shù)學(xué)理.files/image324.gif) ;
;
當(dāng)中學(xué)高三二診模擬數(shù)學(xué)理.files/image194.gif) =6m與
=6m與中學(xué)高三二診模擬數(shù)學(xué)理.files/image194.gif) =10m時(shí)的概率為
=10m時(shí)的概率為中學(xué)高三二診模擬數(shù)學(xué)理.files/image326.gif) ;tesoon
;tesoon
當(dāng)中學(xué)高三二診模擬數(shù)學(xué)理.files/image194.gif) =7m與
=7m與中學(xué)高三二診模擬數(shù)學(xué)理.files/image194.gif) =9m時(shí)的概率為
=9m時(shí)的概率為中學(xué)高三二診模擬數(shù)學(xué)理.files/image328.gif) ;
;
當(dāng)中學(xué)高三二診模擬數(shù)學(xué)理.files/image194.gif) =8m時(shí)的概率為
=8m時(shí)的概率為中學(xué)高三二診模擬數(shù)學(xué)理.files/image330.gif) .…………………………………………(9分)
.…………………………………………(9分)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image332.gif) 的分布列為:
的分布列為:
中學(xué)高三二診模擬數(shù)學(xué)理.files/image194.gif)
5
6
7
8
9
10
11
中學(xué)高三二診模擬數(shù)學(xué)理.files/image156.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image335.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image337.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image339.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image341.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image339.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image337.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image335.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image346.gif) …………………………(12分)
…………………………(12分)
19、(1)圓中學(xué)高三二診模擬數(shù)學(xué)理.files/image348.gif) ,當(dāng)
,當(dāng)中學(xué)高三二診模擬數(shù)學(xué)理.files/image209.gif) 時(shí),點(diǎn)
時(shí),點(diǎn)中學(xué)高三二診模擬數(shù)學(xué)理.files/image351.gif) 在圓上,故當(dāng)且僅當(dāng)直線
在圓上,故當(dāng)且僅當(dāng)直線中學(xué)高三二診模擬數(shù)學(xué)理.files/image200.gif) 過(guò)圓心C時(shí)滿足
過(guò)圓心C時(shí)滿足中學(xué)高三二診模擬數(shù)學(xué)理.files/image207.gif) .
.
中學(xué)高三二診模擬數(shù)學(xué)理.files/image355.gif) 圓心坐標(biāo)為(1,1),
圓心坐標(biāo)為(1,1),中學(xué)高三二診模擬數(shù)學(xué)理.files/image357.gif) …………………………………………………………(3分)
…………………………………………………………(3分)
(2)由中學(xué)高三二診模擬數(shù)學(xué)理.files/image359.gif) ,消去
,消去中學(xué)高三二診模擬數(shù)學(xué)理.files/image361.gif) 可得
可得中學(xué)高三二診模擬數(shù)學(xué)理.files/image363.gif) .
.
中學(xué)高三二診模擬數(shù)學(xué)理.files/image365.gif) 得
得中學(xué)高三二診模擬數(shù)學(xué)理.files/image367.gif) ………………①
………………①
設(shè)中學(xué)高三二診模擬數(shù)學(xué)理.files/image369.gif) ,則
,則中學(xué)高三二診模擬數(shù)學(xué)理.files/image371.gif) ……………………………………(5分)
……………………………………(5分)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image355.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image373.gif) ,即
,即中學(xué)高三二診模擬數(shù)學(xué)理.files/image375.gif) =0.
=0.
又中學(xué)高三二診模擬數(shù)學(xué)理.files/image377.gif) ,
,中學(xué)高三二診模擬數(shù)學(xué)理.files/image379.gif) ,即
,即中學(xué)高三二診模擬數(shù)學(xué)理.files/image381.gif) .
.
中學(xué)高三二診模擬數(shù)學(xué)理.files/image383.gif) .
.
故中學(xué)高三二診模擬數(shù)學(xué)理.files/image385.gif) …………………………………………………………………………(9分)
…………………………………………………………………………(9分)
又中學(xué)高三二診模擬數(shù)學(xué)理.files/image387.gif) (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng)中學(xué)高三二診模擬數(shù)學(xué)理.files/image209.gif) 時(shí)取=)
時(shí)取=)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image390.gif) 即
即中學(xué)高三二診模擬數(shù)學(xué)理.files/image392.gif) ………………②
………………②
由①②知,中學(xué)高三二診模擬數(shù)學(xué)理.files/image392.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image394.gif) 直線
直線中學(xué)高三二診模擬數(shù)學(xué)理.files/image200.gif) 的傾斜角取值范圍為:
的傾斜角取值范圍為:中學(xué)高三二診模擬數(shù)學(xué)理.files/image397.gif) …………………………………………………(12分)
…………………………………………………(12分)
20、解:(1)設(shè)中學(xué)高三二診模擬數(shù)學(xué)理.files/image399.gif) ,
,
(中學(xué)高三二診模擬數(shù)學(xué)理.files/image401.gif) )
)中學(xué)高三二診模擬數(shù)學(xué)理.files/image403.gif) 在[-1,1]上是增函數(shù)………………………………………(3分)
在[-1,1]上是增函數(shù)………………………………………(3分)
(2)中學(xué)高三二診模擬數(shù)學(xué)理.files/image405.gif) ,解得:
,解得:中學(xué)高三二診模擬數(shù)學(xué)理.files/image407.gif) …………………………(7分)
…………………………(7分)
(3)對(duì)所有中學(xué)高三二診模擬數(shù)學(xué)理.files/image409.gif) 恒成立,等價(jià)于
恒成立,等價(jià)于中學(xué)高三二診模擬數(shù)學(xué)理.files/image006.gif) 的最大值不大于
的最大值不大于中學(xué)高三二診模擬數(shù)學(xué)理.files/image412.gif) .
.
又中學(xué)高三二診模擬數(shù)學(xué)理.files/image414.gif) 在[-1,1]上是增函數(shù),
在[-1,1]上是增函數(shù),中學(xué)高三二診模擬數(shù)學(xué)理.files/image006.gif) 在[-1,1]上的最大值為
在[-1,1]上的最大值為中學(xué)高三二診模擬數(shù)學(xué)理.files/image417.gif)
即中學(xué)高三二診模擬數(shù)學(xué)理.files/image419.gif) ,得
,得中學(xué)高三二診模擬數(shù)學(xué)理.files/image421.gif) ,
,
設(shè)中學(xué)高三二診模擬數(shù)學(xué)理.files/image423.gif) ,是關(guān)于
,是關(guān)于中學(xué)高三二診模擬數(shù)學(xué)理.files/image035.gif) 的一次函數(shù),要使
的一次函數(shù),要使中學(xué)高三二診模擬數(shù)學(xué)理.files/image426.gif) 恒成立,
恒成立,
只需中學(xué)高三二診模擬數(shù)學(xué)理.files/image428.gif) 即可,解得:
即可,解得:中學(xué)高三二診模擬數(shù)學(xué)理.files/image430.gif) 或
或中學(xué)高三二診模擬數(shù)學(xué)理.files/image432.gif) 或
或中學(xué)高三二診模擬數(shù)學(xué)理.files/image434.gif) .
.
21、解析:(1)設(shè)中學(xué)高三二診模擬數(shù)學(xué)理.files/image436.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image414.gif) 在
在中學(xué)高三二診模擬數(shù)學(xué)理.files/image234.gif) 處有極值,
處有極值,中學(xué)高三二診模擬數(shù)學(xué)理.files/image440.gif) 即
即中學(xué)高三二診模擬數(shù)學(xué)理.files/image442.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image355.gif) 在點(diǎn)(0,-3)處的切線平行于
在點(diǎn)(0,-3)處的切線平行于中學(xué)高三二診模擬數(shù)學(xué)理.files/image445.gif) 即
即中學(xué)高三二診模擬數(shù)學(xué)理.files/image447.gif)
故中學(xué)高三二診模擬數(shù)學(xué)理.files/image449.gif) …………………………………………………………………(4分)
…………………………………………………………………(4分)
(2)設(shè)中學(xué)高三二診模擬數(shù)學(xué)理.files/image451.gif)
又中學(xué)高三二診模擬數(shù)學(xué)理.files/image453.gif) 時(shí),
時(shí),中學(xué)高三二診模擬數(shù)學(xué)理.files/image455.gif) (遞減)
(遞減)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image457.gif) 時(shí),
時(shí),中學(xué)高三二診模擬數(shù)學(xué)理.files/image459.gif) (遞增)
(遞增)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image394.gif) 曲線
曲線中學(xué)高三二診模擬數(shù)學(xué)理.files/image239.gif) 上任意兩點(diǎn)的連線的斜率恒大于
上任意兩點(diǎn)的連線的斜率恒大于中學(xué)高三二診模擬數(shù)學(xué)理.files/image039.gif) .
.
解不等式中學(xué)高三二診模擬數(shù)學(xué)理.files/image464.gif) 得
得中學(xué)高三二診模擬數(shù)學(xué)理.files/image466.gif) .
.
中學(xué)高三二診模擬數(shù)學(xué)理.files/image468.gif) 或
或中學(xué)高三二診模擬數(shù)學(xué)理.files/image470.gif) …………………………………………………………(8分)
…………………………………………………………(8分)
(3)設(shè)中學(xué)高三二診模擬數(shù)學(xué)理.files/image472.gif) ,則
,則中學(xué)高三二診模擬數(shù)學(xué)理.files/image474.gif) ,
,中學(xué)高三二診模擬數(shù)學(xué)理.files/image476.gif) 時(shí)
時(shí)中學(xué)高三二診模擬數(shù)學(xué)理.files/image478.gif) 為[0,1]上的增函數(shù)
為[0,1]上的增函數(shù)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image480.gif) 的值域是[-4.
的值域是[-4. 中學(xué)高三二診模擬數(shù)學(xué)理.files/image482.gif) ].…………………………(12分)
].…………………………(12分)
22、解析:(1)圓中學(xué)高三二診模擬數(shù)學(xué)理.files/image256.gif) 與
與中學(xué)高三二診模擬數(shù)學(xué)理.files/image264.gif) 彼此外切,令
彼此外切,令中學(xué)高三二診模擬數(shù)學(xué)理.files/image486.gif) 為圓
為圓中學(xué)高三二診模擬數(shù)學(xué)理.files/image256.gif) 的半徑,
的半徑,
中學(xué)高三二診模擬數(shù)學(xué)理.files/image489.gif) 即
即中學(xué)高三二診模擬數(shù)學(xué)理.files/image491.gif) ,
,
兩邊平方并化簡(jiǎn)得中學(xué)高三二診模擬數(shù)學(xué)理.files/image493.gif) ,
,
由題意得,圓中學(xué)高三二診模擬數(shù)學(xué)理.files/image256.gif) 的半徑
的半徑中學(xué)高三二診模擬數(shù)學(xué)理.files/image496.gif) ,
,中學(xué)高三二診模擬數(shù)學(xué)理.files/image498.gif)
即中學(xué)高三二診模擬數(shù)學(xué)理.files/image500.gif) ……………………………………………………………………(5分)
……………………………………………………………………(5分)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image394.gif) 數(shù)列
數(shù)列中學(xué)高三二診模擬數(shù)學(xué)理.files/image503.gif) 是以
是以中學(xué)高三二診模擬數(shù)學(xué)理.files/image505.gif) 為首項(xiàng),以2為公差的等差數(shù)列,
為首項(xiàng),以2為公差的等差數(shù)列,
所以中學(xué)高三二診模擬數(shù)學(xué)理.files/image507.gif) 即
即中學(xué)高三二診模擬數(shù)學(xué)理.files/image509.gif) .………………………………………………(8分)
.………………………………………………(8分)
(2)中學(xué)高三二診模擬數(shù)學(xué)理.files/image511.gif) ,……………………………………………………(10分)
,……………………………………………………(10分)
因?yàn)?sub>中學(xué)高三二診模擬數(shù)學(xué)理.files/image513.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image515.gif) …………………………………………………(12分)
…………………………………………………(12分)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image517.gif)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image519.gif)
所以中學(xué)高三二診模擬數(shù)學(xué)理.files/image278.gif) ………………………………………………………………………………(14分)
………………………………………………………………………………(14分)
中學(xué)高三二診模擬數(shù)學(xué)理.files/image521.gif) 天星教育網(wǎng)(www.tesoon.com) 版權(quán)所有
天星教育網(wǎng)(www.tesoon.com) 版權(quán)所有
天星教育網(wǎng)(www.tesoon.com) 版權(quán)所有
天星教育網(wǎng)(www.tesoon.com) 版權(quán)所有