題目列表(包括答案和解析)
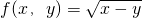； ④f（x，y）=x2+y2．若對任意的
,(
),有唯一 確定的
與之對應，則稱為關于
的二元函數。現定義滿足下列性質的二元函數為關于實數的廣義“距離”：
（1）非負性：
，當且僅當
時取等號；
（2）對稱性：
；
（3）三角形不等式：
對任意的實數
均成立。
今給出下列四個二元函數：①
； ②
；
③
； ④
。
能夠稱為關于實數的廣義“距離”的函數的序號是
若對任意x∈A，y∈B，(
)有唯一確定的f(x，y)與之對應，則稱f(x，y)為關于x，y的二元函數．現定義滿足下列性質的二元函數f(x，y)為關于實數x，y的廣義“距離”：
(1)非負性：f(x，y)≥0，當且僅當x＝y時取等號；
(2)對稱性：f(x，y)＝f(y，x)；
(3)三角形不等式：f(x，y)≤f(x，z)＋f(z，y)對任意的實數z均成立．
今給出三個二元函數，請選出所有能夠成為關于x，y的廣義“距離”的序號：
①f(x，y)＝|x－y|；②f(x，y)＝(x－y)2；③f(x，y)＝
．
________．
若對任意x∈A，y∈B，(
)有唯一確定的f(x，y)與之對應，則稱f(x，y)為關于x，y的二元函數．現定義滿足下列性質的二元函數f(x，y)為關于實數x，y的廣義“距離”：
(1)非負性：f(x，y)≥0，當且僅當x＝y時取等號；
(2)對稱性：f(x，y)＝f(y，x)；
(3)三角形不等式：f(x，y)≤f(x，z)＋f(z，y)對任意的實數z均成立．
今給出三個二元函數，請選出所有能夠成為關于x，y的廣義“距離”的序號：
①f(x，y)＝|x－y)；②f(x，y)＝f(x－y)2；③
．
________．
若對任意x∈A，y∈B，(
)有唯一確定的f(x，y)與之對應，則稱f(x，y)為關于x，y的二元函數．
定義：滿足下列性質的二元函數f(x，y)為關于實數x，y的廣義“距離”：
(1)非負性：f(x，y)≥0，當且僅當x＝y時取等號；
(2)對稱性：f(x，y)＝f(y，x)；
(3)三角形不等式：f(x，y)≤f(x，z)＋f(z，y)對任意的實數z均成立．
給出三個二元函數：①f(x，y)＝(x－y)2；②f(x，y)＝|x－y|；③f(x，y)＝
．
請選出所有能夠成為關于x，y的廣義“距離”的序號________．
一、1～10 DBDAB DBCCB
二、11、2 ；12、2；13、.files/image244.gif)
；14、.files/image246.gif)
；15、伸長 .files/image248.gif)
；伸長 6；左 .files/image250.gif)
三、16 解：.files/image252.gif)
；.files/image254.gif)
--------------6‘
.files/image256.gif)
----------------------------------------8‘
（或證.files/image258.gif)
）
17解： （1） .files/image260.gif)
------------------- 3′
.files/image262.gif)
4′
（2）.files/image264.gif)
6′
.files/image266.gif)
8′
18．（1）記事件A為“任取兩張卡片，將卡片上的函數相加得到的函數是奇函數”，由題意知.files/image268.gif)
4′
（2）ξ可取1，2，3，4. ξ的分布列為
ξ
1
2
3
4
P
.files/image061.gif)
.files/image271.gif)
.files/image273.gif)
.files/image275.gif)
7‘
.files/image277.gif)
8‘
19解： ⑴.files/image279.gif)
4‘
⑵.files/image281.gif)
.files/image283.gif)
6′
.files/image285.gif)
.files/image287.gif)
7′
.files/image289.gif)
8‘
20 解：（1）用反證法（略） 3‘
（2）根據函數圖像分類，當.files/image291.gif)
時，.files/image227.gif)
無最大值；當.files/image294.gif)
時，最大值，且.files/image297.gif)
的最大值為.files/image299.gif)
；
6‘
（3）.files/image301.gif)
，.files/image303.gif)
7‘
.files/image305.gif)
8‘
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com