
題目列表(包括答案和解析)
1.設集合![]() ,則
,則![]() 等于 ( )
等于 ( )
A.{1,2} B.{3,4} C.{1} D.{-2,-1,0,1,2}
設集合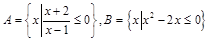 ,則
,則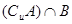 等于 ( )
等于 ( )
A. | B. | C.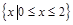 | D.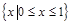 |
設集合 ,則
,則 等于( )
等于( )
(A) (B)
(B) (C)
(C) (D)
(D)

設集合 ,則
,則 等于 ( )
等于 ( )
A.R B. C.
C. D.
D.
設集合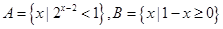 ,則
,則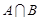 等于 ( )
等于 ( )
A.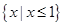 B.
B.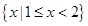 C.
C.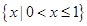 D.
D.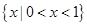
一、選擇題
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
B
D
D
C
A
A
B
A
C
D
二、填空題13.卷.files/image372.gif) ;
14.
;
14.卷.files/image374.gif) ; 15.
; 15.卷.files/image376.gif) ; 16.
; 16.卷.files/image378.gif) .
.
三、解答題
17.(1)卷.files/image380.gif)
卷.files/image382.gif)
卷.files/image384.gif)
卷.files/image386.gif) 兩兩相互垂直, 連結
兩兩相互垂直, 連結卷.files/image388.gif) 并延長交
并延長交卷.files/image390.gif) 于F.
于F.
卷.files/image392.gif)
卷.files/image394.gif)
同理可得卷.files/image396.gif)
卷.files/image398.gif)
卷.files/image400.gif)
卷.files/image402.gif)
卷.files/image404.gif) ------------ (6分)
------------ (6分)
(2)卷.files/image272.gif) 是
是卷.files/image270.gif) 的重心, F是SB的中點
的重心, F是SB的中點
卷.files/image408.gif)
卷.files/image410.gif)
梯形的高卷.files/image412.gif)
卷.files/image414.gif) --- (12分)
--- (12分)
【注】可以用空間向量的方法
18.解:
(1)設通過3次檢測,就可以把3箱含“三聚氰胺”的牛奶全部篩選出來的事件為A
卷.files/image416.gif) 1分
1分
P(A)=卷.files/image418.gif)
卷.files/image416.gif) 5分
5分
所以通過3次檢測,就可以把3箱含“三聚氰胺”的牛奶全部篩選出來的概率為卷.files/image420.gif)
卷.files/image422.gif) …6分
…6分
(2)設最多通過4次檢測,就可以把3箱含“三聚氰胺”的牛奶全部篩選出來的事件為B … 7分
P(B)=卷.files/image424.gif)
卷.files/image416.gif) 11分
11分
所以最多通過4次檢測,就可以把3箱含“三聚氰胺”的牛奶全部篩選出來的概率為卷.files/image138.gif)
卷.files/image422.gif) … 12分
… 12分
19.(1)卷.files/image428.gif) .
.
又卷.files/image430.gif)
卷.files/image432.gif) .
.
卷.files/image434.gif)
卷.files/image436.gif) .………6分
.………6分
(2)
卷.files/image437.gif)
卷.files/image439.gif)
又卷.files/image441.gif) ,
,
卷.files/image443.gif) .從而
.從而
卷.files/image445.gif)
當卷.files/image447.gif) 且同向時,
且同向時,卷.files/image449.gif) .………12分
.………12分
20.解:(1) 卷.files/image451.gif) ,
,
令卷.files/image453.gif) ,由
,由卷.files/image455.gif) 得
得卷.files/image457.gif) 或
或卷.files/image459.gif) .
.卷.files/image461.gif) .
.卷.files/image463.gif)
卷.files/image465.gif) .
.
當卷.files/image467.gif) 時,
時,卷.files/image469.gif) ,當
,當卷.files/image471.gif) 時,
時,卷.files/image473.gif) ,所以
,所以卷.files/image475.gif) 處取極小值,即
處取極小值,即卷.files/image477.gif) …………4分
…………4分
(2)卷.files/image479.gif)
卷.files/image481.gif)
卷.files/image483.gif) 處取得極小值,即
處取得極小值,即卷.files/image485.gif) 由
由卷.files/image487.gif) 即
即卷.files/image489.gif)
卷.files/image491.gif)
卷.files/image493.gif)
卷.files/image495.gif)
卷.files/image497.gif)
卷.files/image499.gif)
由四邊形ABCD是梯形及BC與AD不平行,得卷.files/image501.gif) .有
.有卷.files/image503.gif) 即
即卷.files/image505.gif)
由四邊形ABCD的面積為1,得卷.files/image507.gif) 即
即卷.files/image509.gif) 得
得卷.files/image511.gif) ,從而
,從而卷.files/image513.gif) 得
得卷.files/image515.gif) ……12分
……12分
21.(1)設雙曲線C2的方程為卷.files/image517.gif) = 1,則a2 = 4 ? 1 = 3,再由a2 + b2
= c2得b2 = 1.故C2的方程為
= 1,則a2 = 4 ? 1 = 3,再由a2 + b2
= c2得b2 = 1.故C2的方程為卷.files/image519.gif) = 1. (5分)
= 1. (5分)
(2)將y = kx +卷.files/image521.gif) 代入
代入卷.files/image523.gif) 得(1 +
4k2)x2 + 8
得(1 +
4k2)x2 + 8卷.files/image521.gif) kx + 4 = 0,由直線l與橢圓C1恒有兩個不同的交點得
kx + 4 = 0,由直線l與橢圓C1恒有兩個不同的交點得卷.files/image526.gif) (8
(8卷.files/image521.gif) )2k2 ? 16 (1 + 4k2)
= 16(4k2 ? 1)>0,即k2>
)2k2 ? 16 (1 + 4k2)
= 16(4k2 ? 1)>0,即k2>卷.files/image529.gif) .①(7分)
.①(7分)
將y = kx + 卷.files/image521.gif) 代入
代入卷.files/image532.gif) 得(1 ?
3k2)x2 ? 6
得(1 ?
3k2)x2 ? 6卷.files/image521.gif) kx ? 9 = 0.由直線l與雙曲線C2恒有兩個不同的交點A、B得
kx ? 9 = 0.由直線l與雙曲線C2恒有兩個不同的交點A、B得卷.files/image535.gif) .即k≠
.即k≠卷.files/image537.gif) 且k2<1.②(9分)
且k2<1.②(9分)
設A (xA,yA),B (xB,yB),則xA + xB
= 卷.files/image539.gif) ,xA,xB =
,xA,xB = 卷.files/image541.gif) ,由
,由卷.files/image543.gif) 得xA xB +
yA yB<6,而xA xB +
yA yB = xA xB + (kxA +
得xA xB +
yA yB<6,而xA xB +
yA yB = xA xB + (kxA + 卷.files/image521.gif) )
(kxb +
)
(kxb + 卷.files/image521.gif) )=
(k2 + 1) xA xB +
)=
(k2 + 1) xA xB + 卷.files/image521.gif) k
(xA + xB)
+ 2 = (k2 + 1)?
k
(xA + xB)
+ 2 = (k2 + 1)?卷.files/image546.gif) ,于是
,于是卷.files/image548.gif) <6,即將
<6,即將卷.files/image550.gif) .解此不等式得
.解此不等式得卷.files/image552.gif) 或
或卷.files/image554.gif) .
③ (11分)
.
③ (11分)
由①、②、③得卷.files/image556.gif) ,
,
故k的取值范圍為卷.files/image558.gif)
卷.files/image560.gif) . (12分)
. (12分)
22.(1)卷.files/image562.gif) .
.
(2)卷.files/image564.gif)
卷.files/image566.gif) ,
,
則卷.files/image568.gif) ,
,
卷.files/image570.gif) .
.
(3)卷.files/image572.gif)
卷.files/image574.gif) ,
,
即卷.files/image576.gif) ①
①
又由于卷.files/image578.gif) ,
,
則卷.files/image580.gif) ,
,
兩式相減得卷.files/image582.gif) ,
,
卷.files/image584.gif) ,
,卷.files/image586.gif) 當
當卷.files/image588.gif) 且
且卷.files/image590.gif) 時是增函數,
時是增函數,
卷.files/image586.gif) 的最小值是
的最小值是卷.files/image593.gif) , ②
, ②
由①②得: 卷.files/image595.gif) 成立.
成立.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com