日本成人片在线_久久免费精品视频_国产午夜精品久久久久久免费视_校花撩起jk露出白色内裤国产精品_av影片免费在线观看_国产小视频在线看_最新av免费在线观看_99久久99久久精品国产片_欧美成人猛片aaaaaaa_蜜桃免费网站一区二区三区

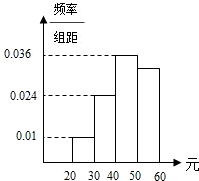學(xué)校為了調(diào)查學(xué)生在課外讀物方面的支出情況，抽出了一個容量為n的樣本，其頻率分布直方圖如圖所示，其中支出在[50，60）元的同學(xué)有30人，則n的值為

 

．

查看答案和解析>>

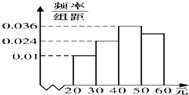13、學(xué)校為了調(diào)查學(xué)生在課外讀物方面的支出情況，抽取了一個容量為100的樣本，其頻率分布直方圖如圖所示，則據(jù)此估計(jì)支出在[50，60）元的同學(xué)的概率為

0.3

．

查看答案和解析>>

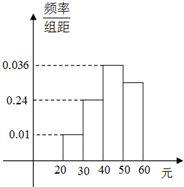學(xué)校為了調(diào)查學(xué)生在課外讀物方面的支出情況，抽出了一個容量為n的樣本，其頻率分布直方圖如圖所示，其中支出在[20，30]元的同學(xué)有30人，則n的值為

300

300

．

查看答案和解析>>

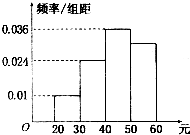學(xué)校為了調(diào)查學(xué)生在課外讀物方面的支出情況，抽出了一個容量為n且支出在[20，60）元的樣本，其頻率分布直方圖如圖所示，根據(jù)此圖估計(jì)學(xué)生在課外讀物方面的支出費(fèi)用的中位數(shù)為

400

9

400

9

元．

查看答案和解析>>

查看答案和解析>>

2009.5

一、選擇題：本大題共10小題，每小題5分，滿分50分．

題號

1

2

3

4

5

6

7

8

9

10

答案

C

A

D

B

A

C

A

B

C

D

二．填空題：本大題共5小題，考生作答4小題，每小題5分，共20分。第11～13題為必做題，第14～15題，考生只能從中選做兩題，若全答只計(jì)前一題的得分。

11：；  12：甲；    13：；  14：；        15：；

解答提示

1．解：則，不符合，則，或，則，成立．

2.解：，故實(shí)部為．

3.解：，則，．

4.解：．

5.解：支出在元的頻率為．．

6.解：由真值表可判斷，若為假命題，則 至少有一假

7.解：當(dāng),由，當(dāng),由， ．

8.解：數(shù)形結(jié)合,將方程組有實(shí)數(shù)解,表示為直線與圓有公共點(diǎn)，則圓心到

　直線距離不超過半徑：．

9.解：設(shè)長方體的同一頂點(diǎn)的三條棱為，對角線在各面上的投影為面對角線長，

　故，，故球的表面積：．

10.解：如右圖，直線和的交點(diǎn)為，

且、，故所求概率為．

11.解：周期．

12. 解：平均數(shù)，方差，，故甲發(fā)揮比乙穩(wěn)定．

13. 解：已知雙曲線，，，且不妨設(shè)

　　由得，又，則為直角三角形

　　故．

14. 解：曲線表示的橢圓標(biāo)準(zhǔn)方程為，可知點(diǎn)、

　　橢圓的焦點(diǎn)，故．

15. 解：為直徑所對的圓周角，則，在中，，

    由等面積法有，故得．

三．解答題：本大題共6小題，共80分。解答應(yīng)寫出文字說明、演算步驟或推證過程。

16. （本小題滿分12分）

解：（Ⅰ）為銳角，

   ，                 

   ；                  …………………4分

   ∴……… 6分

（Ⅱ）由（Ⅰ）可知，，∴        …………………7分

　由正弦定理，可得      …………………9分

  ∴             …………………12分

17. （本小題滿分12分）

解: （I） 用　甲乙丙甲　表示一種傳球方法，（也可用樹形圖表示，如下圖）

　所有傳球方法共有

　　甲乙甲乙；　甲乙甲丙；　　甲乙丙甲；　　甲乙丙乙；

　　甲丙甲乙；　甲丙甲丙；　　甲丙乙甲；　　甲丙乙丙；

　則共有８種傳球方法　　　　　　　　　　        …………………………………………8分

                                        （情況列舉不足或過剩給4分）

（Ⅱ）記求第3次球恰好傳回給甲的事件為，          

由（I）可知共有兩種情況，則

　．　                      …………………………………………12分

18．（本小題滿分14分）

證明：（Ⅰ）證法一：取中點(diǎn)為，連結(jié)，中，…………1分

  ∵，∴且…………2分

又∵且，

∴且 …………3分

四邊形為平行四邊形，∴…………4分

∵平面，平面，

∴平面，　　　        ………………7分

證法二：由圖1可知，…………1分

折疊之后平行關(guān)系不變

∵平面，平面，

∴平面，

同理平面　   …………4分

∵，平面，

　　∴平面平面 　　　　　　　　　…………6分

∵平面，∴平面          …………7分

（Ⅱ）解法1: ∵                     …………8分

      由圖1可知

∵平面平面，平面平面

平面，

∴平面，　　　　　　　　　　　　…………11分

    由圖1可知…………12分

    ∴

    解法2: 由圖1可知，

∵

∴平面，                        …………9分

∵

點(diǎn)到平面的距離等于點(diǎn)到平面的距離為1，…………11分

    由圖1可知…………12分

    ∴

解法3: 過作,垂足為,…………8分

由圖1可知

∵平面平面，

平面平面

平面，

∴平面，　　　　　

∵平面∴，

    平面              …………11分

     由，，

　　，  …………12分

   在中,由等面積法可得…………13分

∴…………14分

19. （本小題滿分14分）

解：（Ⅰ）　已知橢圓的短半軸為，半焦距為，

　由離心率等于　　　　　　　　         …………………………2分

  ∴，　　　　　　　　　                           …………………………３分

  ∴橢圓的上頂點(diǎn)，∴拋物線的焦點(diǎn)為，

　∴拋物線的方程為　                            　…………………………6分

（Ⅱ）設(shè)直線的方程為，，

  ∴  ∴切線、的斜率分別為、　     …………………………8分

  當(dāng)時，即：　                      …………………………9分

   由得： 

  解得或 ①

　∴即：