
題目列表(包括答案和解析)
A.![]() B.
B.![]() C.
C.![]() D.不存在
D.不存在
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
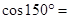 ( )
( )
A.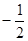 B.
B. C.
C.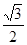 D.
D.
 =(
)
=(
)
A. B.
B. C.
C. D.
D.
一、選擇題
1.D 2.B 3.C 4.D 5.B 6.C 7.C 8.D 9.C 10.D
二、填空題
11.學(xué).files/image091.gif) 12.
12.學(xué).files/image093.gif) 13.
13.學(xué).files/image095.gif) 14.2+
14.2+學(xué).files/image097.gif) 15.
15.學(xué).files/image099.gif)
三、解答題
16.⑴∵學(xué).files/image101.gif) 1分
1分
=學(xué).files/image103.gif) 3分
3分
又由學(xué).files/image105.gif) 得
得學(xué).files/image107.gif) ∴
∴學(xué).files/image109.gif) 5分
5分
故學(xué).files/image111.gif) ,f (x)max=1+2×1=3 6分
,f (x)max=1+2×1=3 6分
⑵學(xué).files/image113.gif) <2在
<2在學(xué).files/image105.gif) 上恒成立
上恒成立學(xué).files/image116.gif)
學(xué).files/image105.gif) 時
時學(xué).files/image118.gif) 9分
9分
結(jié)合⑴知:學(xué).files/image120.gif) 故m的取值范圍是(1,4) 12分
故m的取值范圍是(1,4) 12分
17.⑴連結(jié)AC,△ABC為正△,又E為BC中點,∴AE⊥BC又AD∥BC
∴AE⊥AD,又PA⊥平面ABCD
故AD為PD在平面ABCD內(nèi)的射影,由三垂線定理知:AE⊥PD。 4分
⑵連HA,由EA⊥平面PAD知∠AHE為EH與平面PAD所成線面角 5分
而tan∠AHE=學(xué).files/image122.gif) 故當(dāng)AH最小即AH⊥PD時EH與平面PAD所成角最大
故當(dāng)AH最小即AH⊥PD時EH與平面PAD所成角最大
6分
令A(yù)B=2,則AE=學(xué).files/image097.gif) ,此時
,此時學(xué).files/image125.gif)
∴AH=學(xué).files/image127.gif) ,由平幾知識得PA=2 7分
,由平幾知識得PA=2 7分
因為PA⊥平面ABCD,PA學(xué).files/image129.gif) 平面PAC,所以平面PAC⊥平面ABCD
平面PAC,所以平面PAC⊥平面ABCD
過E作EO⊥AC于O,則EO⊥平面PAC
過O作OS⊥AF于S,連結(jié)ES,則∠ESO
為二面角E―AF―C的平面角 9分
在Rt△AOE中,EO=AE?sin30o=學(xué).files/image131.gif) ,AO=AE?cos30o=
,AO=AE?cos30o=學(xué).files/image133.gif)
又F是PC的中點,在Rt△ASO中,SO=AO?sin45o=學(xué).files/image135.gif)
又SE=學(xué).files/image137.gif) ,在Rt△ESO中,cos∠ESO=
,在Rt△ESO中,cos∠ESO=學(xué).files/image139.gif)
即所求二面角的余弦值為學(xué).files/image141.gif) 12分
12分
注:向量法及其它方法可參照給分。
18.⑴設(shè)平均數(shù)為學(xué).files/image143.gif) ,
,學(xué).files/image145.gif)
即測量50次的平均值為
⑵學(xué).files/image147.gif) 7分
7分
⑶每一次測得數(shù)據(jù)為學(xué).files/image149.gif) 10分
10分
故所求概率學(xué).files/image151.gif) 12分
12分
19.⑴容器底面是邊長為(2-2x)的正三角形,高為x
∴學(xué).files/image153.gif) ∴
∴學(xué).files/image155.gif)
故定義域為學(xué).files/image157.gif)
⑵學(xué).files/image159.gif) ,
,學(xué).files/image161.gif) 5分
5分
令V'=0得x<學(xué).files/image163.gif) 或x>1;V'<0得
或x>1;V'<0得學(xué).files/image165.gif)
∴V在(0,學(xué).files/image163.gif) )和(1,+∞)上單調(diào)遞增,在(
)和(1,+∞)上單調(diào)遞增,在(學(xué).files/image163.gif) ,1)上單調(diào)遞減
,1)上單調(diào)遞減
當(dāng)學(xué).files/image168.gif) 時,x=
時,x=學(xué).files/image163.gif) 時,V最大,Vmax=V(
時,V最大,Vmax=V(學(xué).files/image163.gif) )=
)=學(xué).files/image170.gif)
當(dāng)學(xué).files/image172.gif) 即
即學(xué).files/image174.gif) 時,由V在(0,
時,由V在(0,學(xué).files/image163.gif) )上遞增知
)上遞增知
x=學(xué).files/image176.gif) 時,V最大,Vmax=
時,V最大,Vmax=學(xué).files/image178.gif)
20.⑴由學(xué).files/image180.gif) 得ax2+(
得ax2+(
∴當(dāng)且僅當(dāng)學(xué).files/image182.gif) 時,
時,學(xué).files/image180.gif) 有唯一解x=0,∴
有唯一解x=0,∴學(xué).files/image184.gif)
當(dāng)學(xué).files/image186.gif) 得x1=2,由
得x1=2,由學(xué).files/image188.gif)
∴數(shù)列學(xué).files/image190.gif) 是首項為
是首項為學(xué).files/image192.gif) ,公差為
,公差為學(xué).files/image194.gif) 的等差數(shù)列
的等差數(shù)列
∴學(xué).files/image196.gif) 7分
7分
⑵學(xué).files/image198.gif) 又
又學(xué).files/image200.gif)
∴學(xué).files/image202.gif) 且an>0,a2=
且an>0,a2=學(xué).files/image204.gif)
∴學(xué).files/image206.gif)
即學(xué).files/image208.gif)
當(dāng)n≥2時,學(xué).files/image210.gif)
學(xué).files/image212.gif)
學(xué).files/image214.gif)
故學(xué).files/image216.gif)
21.⑴設(shè)橢圓方程為學(xué).files/image218.gif) ,F(xiàn)(c,0)
,F(xiàn)(c,0)
則AB∶y=x-c代入學(xué).files/image220.gif) 得(a2+b2)x2-
得(a2+b2)x2-
令A(yù)(x1、y1)、B(x2、y2),則學(xué).files/image222.gif)
由學(xué).files/image224.gif) 與
與學(xué).files/image226.gif) 共線
共線
得3(y1+y2)+(x1+x2)=0,又y1=x1-c,y2=x2-c
∴3(x1+x2-學(xué).files/image228.gif)
∴學(xué).files/image230.gif) 即a2=3b2,故
即a2=3b2,故學(xué).files/image232.gif) 7分
7分
⑵由⑴知a2=3b2,橢圓方程學(xué).files/image220.gif) 可化為x2+3y2=3b2
可化為x2+3y2=3b2
設(shè)學(xué).files/image235.gif) =(x,y),則(x,y)=λ(x1,y1)+μ(x2,y2)
=(x,y),則(x,y)=λ(x1,y1)+μ(x2,y2)
∴學(xué).files/image237.gif)
∵M(x,y)在橢圓上
∴(λx1+μx2)2+(λy2+μy2)2=3b2
即λ2(x12+3y12)+μ2(3x22+3y22)+2λμ(x1x2+3y1y2)=3b2 ①
由⑴知,x1+x2=學(xué).files/image239.gif) ,a2=
,a2=學(xué).files/image241.gif) ,b2=
,b2=學(xué).files/image243.gif)
∴x1x2=學(xué).files/image245.gif)
∴x1x2+3y1y2=x1x2+3(x1-c)(x2-c)=4x1x2-3(x1+x2)c+
=學(xué).files/image247.gif)
又x12+3y12=3b2,x22+3y22=3b2代入①得λ2+μ2=1 14分
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com