
題目列表(包括答案和解析)
如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
(Ⅰ)證明PC⊥AD;
(Ⅱ)求二面角A-PC-D的正弦值;
(Ⅲ)設E為棱PA上的點,滿足異面直線BE與CD所成的角為30°,求AE的長.

【解析】解法一:如圖,以點A為原點建立空間直角坐標系,依題意得A(0,0,0),D(2,0,0),C(0,1,0), 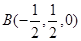 ,P(0,0,2).
,P(0,0,2).

(1)證明:易得 ,
, 于是
于是 ,所以
,所以
(2)  ,
, 設平面PCD的法向量
設平面PCD的法向量 ,
,
則 ,即
,即 .不防設
.不防設 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量 于是
于是 從而
從而 .
.
所以二面角A-PC-D的正弦值為 .
.
(3)設點E的坐標為(0,0,h),其中 ,由此得
,由此得 .
.
由 ,故
,故
所以, ,解得
,解得 ,即
,即 .
.
解法二:(1)證明:由 ,可得
,可得 ,又由
,又由 ,
, ,故
,故 .又
.又 ,所以
,所以 .
.

(2)如圖,作 于點H,連接DH.由
于點H,連接DH.由 ,
, ,可得
,可得 .
.
因此 ,從而
,從而 為二面角A-PC-D的平面角.在
為二面角A-PC-D的平面角.在 中,
中, ,由此得
,由此得 由(1)知
由(1)知 ,故在
,故在 中,
中,
因此 所以二面角
所以二面角 的正弦值為
的正弦值為 .
.
(3)如圖,因為 ,故過點B作CD的平行線必與線段AD相交,設交點為F,連接BE,EF. 故
,故過點B作CD的平行線必與線段AD相交,設交點為F,連接BE,EF. 故 或其補角為異面直線BE與CD所成的角.由于BF∥CD,故
或其補角為異面直線BE與CD所成的角.由于BF∥CD,故 .在
.在 中,
中, 故
故

在 中,由
中,由 ,
, ,
,
可得 .由余弦定理,
.由余弦定理, ,
,
所以 .
.
如圖6,在四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)證明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直線PD與平面PAC所成的角為30°,求四棱錐P-ABCD的體積.

【解析】(Ⅰ)因為
又 是平面PAC內的兩條相較直線,所以BD
是平面PAC內的兩條相較直線,所以BD 平面PAC,
平面PAC,
而 平面PAC,所以
平面PAC,所以 .
.
(Ⅱ)設AC和BD相交于點O,連接PO,由(Ⅰ)知,BD 平面PAC,
平面PAC,
所以 是直線PD和平面PAC所成的角,從而
是直線PD和平面PAC所成的角,從而
 .
.
由BD 平面PAC,
平面PAC, 平面PAC,知
平面PAC,知 .在
.在 中,由
中,由
 ,得PD=2OD.因為四邊形ABCD為等腰梯形,
,得PD=2OD.因為四邊形ABCD為等腰梯形, ,所以
,所以 均為等腰直角三角形,從而梯形ABCD的高為
均為等腰直角三角形,從而梯形ABCD的高為 于是梯形ABCD面積
于是梯形ABCD面積
 在等腰三角形AOD中,
在等腰三角形AOD中,
所以
故四棱錐 的體積為
的體積為 .
.

【點評】本題考查空間直線垂直關系的證明,考查空間角的應用,及幾何體體積計算.第一問只要證明BD 平面PAC即可,第二問由(Ⅰ)知,BD
平面PAC即可,第二問由(Ⅰ)知,BD 平面PAC,所以
平面PAC,所以 是直線PD和平面PAC所成的角,然后算出梯形的面積和棱錐的高,由
是直線PD和平面PAC所成的角,然后算出梯形的面積和棱錐的高,由 算得體積
算得體積
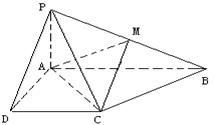
已知四棱錐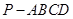 的底面為直角梯形,
的底面為直角梯形,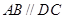 ,
,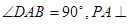 底面
底面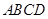 ,且
,且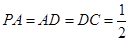 ,
,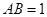 ,
,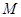 是
是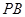 的中點。
的中點。
(1)證明:面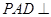 面
面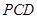 ;
;
(2)求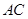 與
與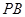 所成的角;
所成的角;
(3)求面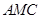 與面
與面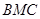 所成二面角的余弦值.
所成二面角的余弦值.
【解析】(1)利用面面垂直的性質,證明CD⊥平面PAD.
(2)建立空間直角坐標系,寫出向量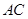 與
與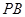 的坐標,然后由向量的夾角公式求得余弦值,從而得所成角的大小.
的坐標,然后由向量的夾角公式求得余弦值,從而得所成角的大小.
(3)分別求出平面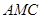 的法向量和面
的法向量和面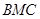 的一個法向量,然后求出兩法向量的夾角即可.
的一個法向量,然后求出兩法向量的夾角即可.
1957年世界人口30億,17年后(即1974年)增加了10億,即達40億;又過13年達到50億;到1999年全世界總人口達到60億.以此速度,人口學專家預測到2025年,世界人口將達到80億;而到2050年人口將超過90億,其中亞洲人口最高,將達到52.68億,北美洲3.92億、歐洲8.28億、拉丁美洲及加勒比地區8.09億,非洲17.68億.
有一位同學根據以上提供的數據制作了三幅統計圖(如圖1,圖2,圖3),請根據這些圖完成問題:
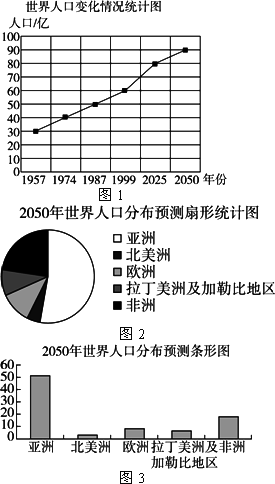
(1)三副統計圖分別表示了什么內容?
(2)從哪幅統計圖中最能看出世界人口的總體變化情況?
(3)2050年非洲人口大約將達到多少億?你是從哪幅統計圖中得到這個數據的?
(4)2050年亞洲人口比其他各洲人口的總和還要多,你從哪幅統計圖中可以明顯地得到這個結論?
(5)從全世界人口的快速增長中,你得到什么啟發?并請發表一下你的感想!
數列 首項
首項 ,前
,前 項和
項和 滿足等式
滿足等式 (常數
(常數 ,
, ……)
……)
(1)求證: 為等比數列;
為等比數列;
(2)設數列 的公比為
的公比為 ,作數列
,作數列 使
使 (
( ……),求數列
……),求數列 的通項公式.
的通項公式.
(3)設 ,求數列
,求數列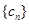 的前
的前 項和
項和 .
.
【解析】第一問利用由 得
得
兩式相減得
故 時,
時,
從而 又
又 即
即 ,而
,而
從而 故
故
第二問中,
 又
又 故
故 為等比數列,通項公式為
為等比數列,通項公式為
第三問中,
 兩邊同乘以
兩邊同乘以
利用錯位相減法得到和。
(1)由 得
得
兩式相減得
故 時,
時,
從而 ………………3分
………………3分
又 即
即 ,而
,而
從而 故
故
 對任意
對任意 ,
, 為常數,即
為常數,即 為等比數列………………5分
為等比數列………………5分
(2)
 ……………………7分
……………………7分
又 故
故 為等比數列,通項公式為
為等比數列,通項公式為 ………………9分
………………9分
(3)
 兩邊同乘以
兩邊同乘以
 ………………11分
………………11分
兩式相減得

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com