日本成人片在线_久久免费精品视频_国产午夜精品久久久久久免费视_校花撩起jk露出白色内裤国产精品_av影片免费在线观看_国产小视频在线看_最新av免费在线观看_99久久99久久精品国产片_欧美成人猛片aaaaaaa_蜜桃免费网站一区二区三区

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

（Ⅰ）求證：；
（Ⅱ）化簡：．

查看答案和解析>>

（Ⅰ）求證：；
（Ⅱ）利用第（Ⅰ）問的結(jié)果證明C_n¹+2C_n²+3C_n³+…+nC_nⁿ=n•2^n-1；  
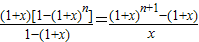（Ⅲ）其實(shí)我們常借用構(gòu)造等式，對同一個(gè)量算兩次的方法來證明組合等式，譬如：（1+x）¹+（1+x）²+（1+x）³+…+（1+x）ⁿ=；，由左邊可求得x²的系數(shù)為C₂²+C₃²+C₄²+…+C_n²，利用右式可得x²的系數(shù)為C_n+1³，所以C₂²+C₃²+C₄²+…+C_n²=C_n+1³．請利用此方法證明：（C_2n）²-（C_2n¹）²+（C_2n²）²-（C_2n³）²+…+（C_2n²ⁿ）²=（-1）ⁿC_2nⁿ．

查看答案和解析>>

理科部分

一、選擇題（本大題共12小題，每小題5分，共60分）

     BAACA         CDBCD       AC

二、填空題（本大題共4小題，每小題4分，共16分）

     13．25        14．        15．8         16．

三、解答題

17．（本小題滿分12分）

    解：（I）

   （Ⅱ）

18．（本小題滿分12分）

    解：（I）依題意，每場比賽獲得的門票收入數(shù)組成首項(xiàng)為40，公差為10的等差數(shù)列，

設(shè)此數(shù)列為，則易知

    此次決賽共比賽了5場。

   （Ⅱ）由

    若要獲得的門票收入不少于390萬元，則至少要比賽6場。

    ①若比賽共進(jìn)行了6場，則前5場比賽的比分必為2：3，且第6場比賽為領(lǐng)先一場的

球隊(duì)獲勝，其概率

    ②若比賽共進(jìn)行了7場，則前6場勝負(fù)為3：3，則概率

    門票收入不少于390萬元的概率為

19．（本小題滿分12分）

    解：方法一（向量法）；

   （I）證明：以點(diǎn)為原點(diǎn)，棱所

在的直線分別為軸和軸建立空間直角坐標(biāo)系

（右手系），設(shè)，則，

    又已知，可求得以下各點(diǎn)的

坐標(biāo)為

   （Ⅱ）已知是直四棱柱，

    ，又由（I）知，

    即是平面的法向量。

    設(shè)平面的法向量為則且

    由圖形可知，二面角的平面為銳角，

    二面角的大小為

方法二（綜合法）：

    （I）是直四棱柱， 

   （Ⅱ）在內(nèi)，過點(diǎn)作的垂線，  交點(diǎn)，連結(jié)。

    由（I）知

垂線定理知，

    就是二面角的平面角。

    同（I）一樣，不妨設(shè)

    在內(nèi)，

    二面角的大小為

20．（本小題滿分12分）

    解：（I）

    令

    顯然當(dāng)

   （Ⅱ）①當(dāng)時(shí)，  函數(shù)在上是單調(diào)減函數(shù)，

在上的最小值 ， 

    又

    綜上，對任意

本問也可以這樣證：

   （Ⅱ）函數(shù)在上單調(diào)遞增，在和上單調(diào)遞減，

對任意

21．（本小題滿分12分）

    解：（I）設(shè)橢圓的方程為橢圓方程化為將點(diǎn)代入，解得，橢圓的方程為

   （Ⅱ）顯然，直線存在斜率（否則不滿足題意，5分），設(shè)其斜率為，則直線的方程為。代入橢圓的方程，消去并整理得

    由方程判別式，  得   ①

    設(shè)兩點(diǎn)的坐標(biāo)為，則由韋達(dá)定理得

     將上面使用韋達(dá)定理所得的結(jié)果代入，并去分

母整理（注意在方程兩邊先約去9可以簡化計(jì)算）得

    檢驗(yàn)①式，均符合；再檢驗(yàn)當(dāng)時(shí)，直線是否與橢圓相交于左右兩個(gè)頂點(diǎn)，顯然直線過橢圓的右頂點(diǎn)。

    不滿足題意，舍去 

    直線的方程為

22．（本小題滿分14分）

    解：（I）方法一：當(dāng)時(shí)，顯然由已知可得成立。

    假設(shè)時(shí)成立，即

    則當(dāng)時(shí)，根據(jù)題意有

    當(dāng)時(shí)，成立。

    根據(jù)數(shù)學(xué)歸納法可知，對任意，成立

    方法二：

    ……，， 將這個(gè)等式累乘（相乘），得

    將代入得   

    檢驗(yàn)當(dāng)時(shí)，上式也成立， 

    方法三：

   （Ⅱ）由（I）知

    又由

    （Ⅲ）當(dāng)時(shí)，由（Ⅱ）可知，有不等式

    成立

    將這個(gè)同向不等式累加起來，得