
題目列表(包括答案和解析)
若![]() ,求
,求![]() 的值.
的值.
若![]() ,求
,求![]() 的值.
的值.
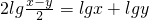 ,求
,求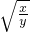 的值.
的值.若![]() ,求
,求![]() 的值.
的值.
若![]() ,求
,求![]() 的值.
的值.
一. ADBCA CABBA BC
二.
13.3; 14.(-∞,4]; 15. 量檢測題--數(shù)學(xué)文.files/image160.gif) ; 16.
; 16. 量檢測題--數(shù)學(xué)文.files/image162.gif) .
.
三.
17. 解:解:由量檢測題--數(shù)學(xué)文.files/image107.gif) ,得
,得量檢測題--數(shù)學(xué)文.files/image164.gif) …3分
…3分
量檢測題--數(shù)學(xué)文.files/image166.gif)
量檢測題--數(shù)學(xué)文.files/image168.gif) ………………6分
………………6分
又量檢測題--數(shù)學(xué)文.files/image169.gif)
量檢測題--數(shù)學(xué)文.files/image171.gif) =
= 量檢測題--數(shù)學(xué)文.files/image173.gif) 。………10分
。………10分
18. 解:(I)分別記“客人游覽甲景點(diǎn)”,“客人游覽乙景點(diǎn)”,“客人游覽丙景點(diǎn)”為事件A1,A2,A3.由已知A1,A2,A3相互獨(dú)立,P(A1)= 0.4,P(A2)= 0.5,P(A3)= 0.6.
P(ξ= 3)= P(A1?A2?A3)+P(A1?A2?A3)
= P(A1)P(A2)P(A3)+P(A1)P(A2)P(A3))
= 2×0.4×0.5×0.6=
(Ⅱ)客人游覽的景點(diǎn)數(shù)的可能取值為0,1,2,3.相應(yīng)地,客人沒有游覽的景點(diǎn)數(shù)的可能取值為3,2,1,0,所以ξ的可能取值為1,3.∴P(ξ= 1)= 1-0.24= 0.76. ………12分
19、解:解法一:(Ⅰ)取量檢測題--數(shù)學(xué)文.files/image175.gif) 中點(diǎn)
中點(diǎn)量檢測題--數(shù)學(xué)文.files/image177.gif) ,連結(jié)
,連結(jié)量檢測題--數(shù)學(xué)文.files/image179.gif) .
.
量檢測題--數(shù)學(xué)文.files/image181.gif) 為正三角形,
為正三角形,量檢測題--數(shù)學(xué)文.files/image183.gif) .
.
量檢測題--數(shù)學(xué)文.files/image185.gif) 正三棱柱
正三棱柱量檢測題--數(shù)學(xué)文.files/image187.gif) 中,平面
中,平面量檢測題--數(shù)學(xué)文.files/image189.gif) 平面
平面量檢測題--數(shù)學(xué)文.files/image191.gif) ,
,
量檢測題--數(shù)學(xué)文.files/image192.gif)
量檢測題--數(shù)學(xué)文.files/image194.gif) 平面
平面量檢測題--數(shù)學(xué)文.files/image191.gif) .
.
連結(jié)量檢測題--數(shù)學(xué)文.files/image197.gif) ,在正方形
,在正方形量檢測題--數(shù)學(xué)文.files/image199.gif) 中,
中,量檢測題--數(shù)學(xué)文.files/image201.gif) 分別為
分別為
量檢測題--數(shù)學(xué)文.files/image203.gif) 的中點(diǎn),
的中點(diǎn),
量檢測題--數(shù)學(xué)文.files/image205.gif) ,
,
量檢測題--數(shù)學(xué)文.files/image207.gif) .………………………………….3分
.………………………………….3分
在正方形量檢測題--數(shù)學(xué)文.files/image209.gif) 中,
中,量檢測題--數(shù)學(xué)文.files/image211.gif) ,
,
量檢測題--數(shù)學(xué)文.files/image213.gif) 平面
平面量檢測題--數(shù)學(xué)文.files/image215.gif) .………………………………….5分
.………………………………….5分
(Ⅱ)設(shè)量檢測題--數(shù)學(xué)文.files/image217.gif) 與
與量檢測題--數(shù)學(xué)文.files/image219.gif) 交于點(diǎn)
交于點(diǎn)量檢測題--數(shù)學(xué)文.files/image221.gif) ,在平面
,在平面量檢測題--數(shù)學(xué)文.files/image215.gif) 中,作
中,作量檢測題--數(shù)學(xué)文.files/image224.gif) 于
于量檢測題--數(shù)學(xué)文.files/image226.gif) ,連結(jié)
,連結(jié)量檢測題--數(shù)學(xué)文.files/image228.gif) ,由(Ⅰ)得
,由(Ⅰ)得量檢測題--數(shù)學(xué)文.files/image230.gif) 平面
平面量檢測題--數(shù)學(xué)文.files/image215.gif) .
.
量檢測題--數(shù)學(xué)文.files/image233.gif) ,
,
量檢測題--數(shù)學(xué)文.files/image235.gif) 為二面角
為二面角量檢測題--數(shù)學(xué)文.files/image237.gif) 的平面角.………………………………….9分
的平面角.………………………………….9分
在量檢測題--數(shù)學(xué)文.files/image239.gif) 中,由等面積法可求得
中,由等面積法可求得量檢測題--數(shù)學(xué)文.files/image241.gif) ,
,
又量檢測題--數(shù)學(xué)文.files/image243.gif) ,
,
量檢測題--數(shù)學(xué)文.files/image245.gif) .
.
所以二面角量檢測題--數(shù)學(xué)文.files/image237.gif) 的正弦值
的正弦值量檢測題--數(shù)學(xué)文.files/image248.gif) .………………………………….12分
.………………………………….12分
解法二:(Ⅰ)取量檢測題--數(shù)學(xué)文.files/image175.gif) 中點(diǎn)
中點(diǎn)量檢測題--數(shù)學(xué)文.files/image177.gif) ,連結(jié)
,連結(jié)量檢測題--數(shù)學(xué)文.files/image179.gif) .
.
量檢測題--數(shù)學(xué)文.files/image181.gif) 為正三角形,
為正三角形,量檢測題--數(shù)學(xué)文.files/image183.gif) .$
.$
量檢測題--數(shù)學(xué)文.files/image255.gif) 平面
平面量檢測題--數(shù)學(xué)文.files/image191.gif) .
.
取量檢測題--數(shù)學(xué)文.files/image258.gif) 中點(diǎn)
中點(diǎn)量檢測題--數(shù)學(xué)文.files/image260.gif) ,以
,以量檢測題--數(shù)學(xué)文.files/image177.gif) 為原點(diǎn),
為原點(diǎn),量檢測題--數(shù)學(xué)文.files/image263.gif) ,
,量檢測題--數(shù)學(xué)文.files/image265.gif) ,
,量檢測題--數(shù)學(xué)文.files/image267.gif) 的方向?yàn)?sub>
的方向?yàn)?sub>量檢測題--數(shù)學(xué)文.files/image269.gif) 軸的正方向建立空間直角坐標(biāo)系,則
軸的正方向建立空間直角坐標(biāo)系,則量檢測題--數(shù)學(xué)文.files/image271.gif) ,
,量檢測題--數(shù)學(xué)文.files/image273.gif) ,
,量檢測題--數(shù)學(xué)文.files/image275.gif) ,
,量檢測題--數(shù)學(xué)文.files/image277.gif) ,
,量檢測題--數(shù)學(xué)文.files/image279.gif) …….3分
…….3分
量檢測題--數(shù)學(xué)文.files/image281.gif) ,
,量檢測題--數(shù)學(xué)文.files/image283.gif) ,
,量檢測題--數(shù)學(xué)文.files/image285.gif) .
.
量檢測題--數(shù)學(xué)文.files/image287.gif) ,
,量檢測題--數(shù)學(xué)文.files/image289.gif) ,
,
量檢測題--數(shù)學(xué)文.files/image290.gif)
量檢測題--數(shù)學(xué)文.files/image292.gif) ,
,量檢測題--數(shù)學(xué)文.files/image294.gif) .
.
量檢測題--數(shù)學(xué)文.files/image213.gif) 平面
平面量檢測題--數(shù)學(xué)文.files/image215.gif) .………………………………….6分
.………………………………….6分
(Ⅱ)設(shè)平面量檢測題--數(shù)學(xué)文.files/image298.gif) 的法向量為
的法向量為量檢測題--數(shù)學(xué)文.files/image300.gif) .
.
量檢測題--數(shù)學(xué)文.files/image302.gif) ,
,量檢測題--數(shù)學(xué)文.files/image304.gif) .
.
量檢測題--數(shù)學(xué)文.files/image306.gif) ,
,量檢測題--數(shù)學(xué)文.files/image308.gif) ,
,
量檢測題--數(shù)學(xué)文.files/image310.gif)
量檢測題--數(shù)學(xué)文.files/image312.gif)
量檢測題--數(shù)學(xué)文.files/image314.gif)
令量檢測題--數(shù)學(xué)文.files/image316.gif) 得
得量檢測題--數(shù)學(xué)文.files/image318.gif) 為平面
為平面量檢測題--數(shù)學(xué)文.files/image298.gif) 的一個法向量.…………………………9分
的一個法向量.…………………………9分
由(Ⅰ)知量檢測題--數(shù)學(xué)文.files/image230.gif) 平面
平面量檢測題--數(shù)學(xué)文.files/image215.gif) ,
,
量檢測題--數(shù)學(xué)文.files/image323.gif) 為平面
為平面量檢測題--數(shù)學(xué)文.files/image215.gif) 的法向量.
的法向量.
量檢測題--數(shù)學(xué)文.files/image326.gif) ,
,量檢測題--數(shù)學(xué)文.files/image328.gif) .
.
量檢測題--數(shù)學(xué)文.files/image330.gif) 二面角
二面角量檢測題--數(shù)學(xué)文.files/image237.gif) 的正弦值
的正弦值量檢測題--數(shù)學(xué)文.files/image248.gif) …………………………12
…………………………12
20.
解:(1)由已知得量檢測題--數(shù)學(xué)文.files/image333.gif) 解得
解得量檢測題--數(shù)學(xué)文.files/image335.gif) .
.
設(shè)數(shù)列量檢測題--數(shù)學(xué)文.files/image032.gif) 的公比為
的公比為量檢測題--數(shù)學(xué)文.files/image338.gif) ,由
,由量檢測題--數(shù)學(xué)文.files/image335.gif) ,可得
,可得量檢測題--數(shù)學(xué)文.files/image341.gif) .
.
又量檢測題--數(shù)學(xué)文.files/image121.gif) ,可知
,可知量檢測題--數(shù)學(xué)文.files/image344.gif) ,
,
即量檢測題--數(shù)學(xué)文.files/image346.gif) ,
解得
,
解得量檢測題--數(shù)學(xué)文.files/image348.gif) .
.
由題意得量檢測題--數(shù)學(xué)文.files/image350.gif) .
.量檢測題--數(shù)學(xué)文.files/image352.gif) .
故數(shù)列
.
故數(shù)列量檢測題--數(shù)學(xué)文.files/image032.gif) 的通項(xiàng)為
的通項(xiàng)為量檢測題--數(shù)學(xué)文.files/image355.gif) .…………6
.…………6
(2)由于量檢測題--數(shù)學(xué)文.files/image126.gif)
由(1)得量檢測題--數(shù)學(xué)文.files/image358.gif)
量檢測題--數(shù)學(xué)文.files/image360.gif) 又
又量檢測題--數(shù)學(xué)文.files/image362.gif)
量檢測題--數(shù)學(xué)文.files/image364.gif) 是等差數(shù)列.
是等差數(shù)列.
量檢測題--數(shù)學(xué)文.files/image366.gif) =
=量檢測題--數(shù)學(xué)文.files/image368.gif) =
=量檢測題--數(shù)學(xué)文.files/image370.gif)
故量檢測題--數(shù)學(xué)文.files/image372.gif) .…………………………12
.…………………………12
21.解:解:(Ⅰ)由題意知f′(x)= ax2+bx-a2,且f′(x)= 0的兩根為x1、x2.
∴x1+x2= - x1x2= -a.
∴(x2-x1)2= (x2+x1)2-4x1x2= 4.
∴()2+
∴b2= (4-
(Ⅱ)由(1)知b2= (4-
令函數(shù)g(a)= (4-
g′(a)=
-
令g'(a)= 0 ∴a1= 0,a2= .
函數(shù)g(a)在(0,)上為增函數(shù),(,1)上為減函數(shù).
∴g(a)max= g()= .
∴b2≤.
∴|b|≤.…………………………12分
22.解:(Ⅰ)由雙曲線的定義可知,曲線量檢測題--數(shù)學(xué)文.files/image141.gif) 是以
是以量檢測題--數(shù)學(xué)文.files/image135.gif) 為焦點(diǎn)的雙曲線的左支,且
為焦點(diǎn)的雙曲線的左支,且量檢測題--數(shù)學(xué)文.files/image376.gif) ,易知
,易知量檢測題--數(shù)學(xué)文.files/image378.gif)
故曲線量檢測題--數(shù)學(xué)文.files/image141.gif) 的方程為
的方程為量檢測題--數(shù)學(xué)文.files/image380.gif) …………………………3
…………………………3
設(shè)量檢測題--數(shù)學(xué)文.files/image382.gif) ,由題意建立方程組
,由題意建立方程組量檢測題--數(shù)學(xué)文.files/image384.gif)
消去量檢測題--數(shù)學(xué)文.files/image386.gif) ,得
,得量檢測題--數(shù)學(xué)文.files/image388.gif)
又已知直線與雙曲線左支交于兩點(diǎn)量檢測題--數(shù)學(xué)文.files/image145.gif) ,有
,有
量檢測題--數(shù)學(xué)文.files/image391.gif) 解得
解得量檢測題--數(shù)學(xué)文.files/image393.gif) ………………5
………………5
∵ 量檢測題--數(shù)學(xué)文.files/image395.gif)
量檢測題--數(shù)學(xué)文.files/image397.gif)
量檢測題--數(shù)學(xué)文.files/image399.gif)
量檢測題--數(shù)學(xué)文.files/image401.gif)
依題意得 量檢測題--數(shù)學(xué)文.files/image403.gif)
量檢測題--數(shù)學(xué)文.files/image405.jpg) 整理后得
整理后得量檢測題--數(shù)學(xué)文.files/image407.gif)
∴量檢測題--數(shù)學(xué)文.files/image409.gif) 或
或量檢測題--數(shù)學(xué)文.files/image411.gif) 但
但量檢測題--數(shù)學(xué)文.files/image393.gif) ∴
∴量檢測題--數(shù)學(xué)文.files/image414.gif)
故直線量檢測題--數(shù)學(xué)文.files/image416.gif) 的方程為
的方程為量檢測題--數(shù)學(xué)文.files/image418.gif) …………………………8
…………………………8
設(shè)量檢測題--數(shù)學(xué)文.files/image420.gif) ,由已知
,由已知量檢測題--數(shù)學(xué)文.files/image152.gif) ,得
,得量檢測題--數(shù)學(xué)文.files/image423.gif)
∴量檢測題--數(shù)學(xué)文.files/image425.gif) ,
,量檢測題--數(shù)學(xué)文.files/image427.gif)
又量檢測題--數(shù)學(xué)文.files/image429.gif) ,
,量檢測題--數(shù)學(xué)文.files/image431.gif)
∴點(diǎn)量檢測題--數(shù)學(xué)文.files/image433.gif)
將點(diǎn)量檢測題--數(shù)學(xué)文.files/image099.gif) 的坐標(biāo)代入曲線
的坐標(biāo)代入曲線量檢測題--數(shù)學(xué)文.files/image141.gif) 的方程,得
的方程,得量檢測題--數(shù)學(xué)文.files/image436.gif) 得
得量檢測題--數(shù)學(xué)文.files/image438.gif) ,
,
但當(dāng)量檢測題--數(shù)學(xué)文.files/image440.gif) 時,所得的點(diǎn)在雙曲線的右支上,不合題意
時,所得的點(diǎn)在雙曲線的右支上,不合題意
∴量檢測題--數(shù)學(xué)文.files/image442.gif) .…………………………10
.…………………………10
點(diǎn)量檢測題--數(shù)學(xué)文.files/image099.gif) 的坐標(biāo)為
的坐標(biāo)為量檢測題--數(shù)學(xué)文.files/image444.gif)
量檢測題--數(shù)學(xué)文.files/image099.gif) 到
到量檢測題--數(shù)學(xué)文.files/image416.gif) 的距離為
的距離為量檢測題--數(shù)學(xué)文.files/image446.gif)
∴量檢測題--數(shù)學(xué)文.files/image156.gif) 的面積
的面積量檢測題--數(shù)學(xué)文.files/image449.gif) …………………………12
…………………………12
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com