
題目列表(包括答案和解析)
| a |
| b |
| a |
| 3 |
| b |
| a |
| b |
| π |
| 2 |
已知函數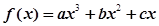 在
在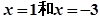 處取得極值,
處取得極值,
且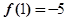
(1) 求函數的解析式;
(2) 若在區間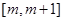 上單調遞增,求
上單調遞增,求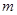 的取值范圍
的取值范圍
二次函數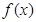 的最小值為1,且
的最小值為1,且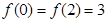 .
.
(Ⅰ)求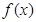 的解析式;
的解析式;
(Ⅱ)若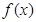 在區間
在區間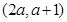 上不單調,求
上不單調,求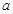 的取值范圍.
的取值范圍.
已知冪函數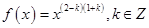 ,且
,且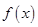 在
在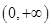 上單調遞增.
上單調遞增.
(1)求實數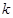 的值,并寫出相應的函數
的值,并寫出相應的函數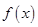 的解析式;
的解析式;
(2)若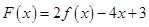 在區間
在區間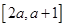 上不單調,求實數
上不單調,求實數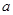 的取值范圍;
的取值范圍;
(3)試判斷是否存在正數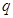 ,使函數
,使函數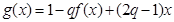 在區間
在區間 上的值域為
上的值域為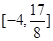 若存在,求出
若存在,求出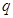 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
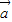 ,
,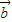 是兩個向量,且
是兩個向量,且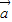 =(1,
=(1,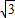 cosx),
cosx),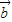 =(cos2x,sinx),x∈R,定義:y=
=(cos2x,sinx),x∈R,定義:y=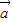 •
•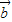 .
.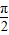 ],求函數y=f(x)的最大值、最小值及其相應的x的值.
],求函數y=f(x)的最大值、最小值及其相應的x的值.一、填空題:
1、 2、(1.5,0)
3、
2、(1.5,0)
3、 4、95%
4、95%
5、 6、大前提 7、18
6、大前提 7、18
8、4 9、 10、4 11、
10、4 11、 12、
12、 13、②③ 14、
13、②③ 14、
二、解答題:
15. (14分) 解:設 ,而
,而 即
即
則

16、(14分)解: 一般性的命題為
證明:左邊

暈機
不暈機
合計
男
24
31
55
女
8
26
34
合計
32
57
89
所以左邊等于右邊
17、(15分).根據題意,列出列聯表如下:
提出統計假設, :在惡劣氣候飛行中男人與女人一樣容易暈機則
:在惡劣氣候飛行中男人與女人一樣容易暈機則

 ,故我們有90%的把握認為在這次航程中男人比女人更容易暈機.
,故我們有90%的把握認為在這次航程中男人比女人更容易暈機.
18、(15分)解: (1) 散點圖略
(2) 



 ;
; 
所求的回歸方程為 
(3) 當 ,
, 
預測生產100噸甲產品的生產能耗比技改前降低 (噸)
(噸)
19、(16分)解:(I)由函數的圖像經過點(0,2)可知, ,
,
 ,∵
,∵ 在點M(-1,f(-1))處的切線方程為
在點M(-1,f(-1))處的切線方程為 .
.
 ,
,
(II)


20、(14分)解:(1) ∴OAPB的正方形
∴OAPB的正方形
由
 ∴P點坐標為(
∴P點坐標為( )
)
(2)設A(x1,y1),B(x2,y2)
則PA、PB的方程分別為 ,而PA、PB交于P(x0,y0)
,而PA、PB交于P(x0,y0)
即x1x0+y1y0=4,x2x0+y2y0=4,∴AB的直線方程為:x0x+y0y=4
(3)由 、
、



當且僅當 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com