
題目列表(包括答案和解析)
(09年湖北黃岡聯(lián)考理)(14分)設(shè)M是由滿足下列條件的函數(shù)![]() 構(gòu)成的集合:“①方程
構(gòu)成的集合:“①方程![]() 有實(shí)數(shù)根;②函數(shù)
有實(shí)數(shù)根;②函數(shù)![]() 的導(dǎo)數(shù)
的導(dǎo)數(shù)![]() 滿足
滿足![]() ”
”
(1)判斷函數(shù)![]() 是否是集合M中的元素,并說(shuō)明理由;
是否是集合M中的元素,并說(shuō)明理由;
(2)若集合M中的元素具有下面的性質(zhì):“若![]() 的定義域?yàn)镈,則對(duì)于任意
的定義域?yàn)镈,則對(duì)于任意![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立”
成立”
試用這一性質(zhì)證明:方程![]() 只有一個(gè)實(shí)數(shù)根;
只有一個(gè)實(shí)數(shù)根;
(3)設(shè)![]() 是方程
是方程![]() 的實(shí)數(shù)根,求證:對(duì)于
的實(shí)數(shù)根,求證:對(duì)于![]() 定義域中的任意的
定義域中的任意的![]() ,當(dāng)
,當(dāng)![]() 且
且![]() 時(shí),
時(shí),![]()
(Ⅰ)判斷函數(shù)f(x)=![]() +
+![]() 是否是集合M中的元素,并說(shuō)明理由;
是否是集合M中的元素,并說(shuō)明理由;
(Ⅱ)集合M中的元素f(x)具有下面的性質(zhì):若f(x)的定義域?yàn)镈,則對(duì)于任意[m,n]![]() D,都存在x0∈[m,n],使得等式f(n)-f(m)=(n-m)f′(x0)成立,試用這一性質(zhì)證明:方程f(x)-x=0只有一個(gè)實(shí)數(shù)根;
D,都存在x0∈[m,n],使得等式f(n)-f(m)=(n-m)f′(x0)成立,試用這一性質(zhì)證明:方程f(x)-x=0只有一個(gè)實(shí)數(shù)根;
(Ⅲ)設(shè)x1是方程f(x)-x=0的實(shí)數(shù)根,求證:對(duì)于f(x)定義域中任意的x2,x3,當(dāng)|x2-x1|<1,且|x3-x1|<1時(shí),|f(x3)-f(x2)|<2.
(本小題滿分13分)
設(shè)M是由滿足下列條件的函數(shù) 構(gòu)成的集合:“①方程
構(gòu)成的集合:“①方程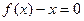 有實(shí)數(shù)根;②函數(shù)
有實(shí)數(shù)根;②函數(shù) 的導(dǎo)數(shù)
的導(dǎo)數(shù)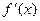 滿足
滿足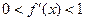 ”.
”.
(1)判斷函數(shù) 是否是集合M中的元素,并說(shuō)明理由;
是否是集合M中的元素,并說(shuō)明理由;
(2)若集合M中的元素具有下面的性質(zhì):“若 的定義域?yàn)镈,則對(duì)于任意
的定義域?yàn)镈,則對(duì)于任意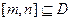 ,都存在
,都存在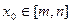 ,使得等式
,使得等式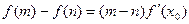 成立”,
成立”, 試用這一性質(zhì)證明:方程
試用這一性質(zhì)證明:方程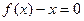 只有一個(gè)實(shí)數(shù)根;
只有一個(gè)實(shí)數(shù)根;
(3)設(shè)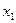 是方程
是方程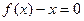 的實(shí)
的實(shí) 數(shù)根,求證:對(duì)于
數(shù)根,求證:對(duì)于 定義域中的任意的
定義域中的任意的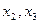 ,當(dāng)
,當(dāng)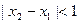 且
且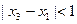 時(shí),
時(shí),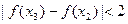 .
.
(本小題滿分13分)
設(shè)M是由滿足下列條件的函數(shù) 構(gòu)成的集合:“①方程
構(gòu)成的集合:“①方程 有實(shí)數(shù)根;②函數(shù)
有實(shí)數(shù)根;②函數(shù) 的導(dǎo)數(shù)
的導(dǎo)數(shù) 滿足
滿足 ”.
”.
(1)判斷函數(shù) 是否是集合M中的元素,并說(shuō)明理由;
是否是集合M中的元素,并說(shuō)明理由;
(2)若集合M中的元素具有下面的性質(zhì):“若 的定義域?yàn)镈,則對(duì)于任意
的定義域?yàn)镈,則對(duì)于任意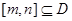 ,都存在
,都存在 ,使得等式
,使得等式 成立”,試用這一性質(zhì)證明:方程
成立”,試用這一性質(zhì)證明:方程 只有一個(gè)實(shí)數(shù)根;
只有一個(gè)實(shí)數(shù)根;
(3)設(shè)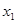 是方程
是方程 的實(shí)數(shù)根,求證:對(duì)于
的實(shí)數(shù)根,求證:對(duì)于 定義域中的任意的
定義域中的任意的 ,當(dāng)
,當(dāng) 且
且 時(shí),
時(shí),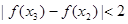 .
.
(Ⅰ)判斷函數(shù)f(x)=![]() 是否是集合M中的元素,并說(shuō)明理由;
是否是集合M中的元素,并說(shuō)明理由;
(Ⅱ )集合M中的元素f(x)具有下面的性質(zhì):“若f(x)的定義域?yàn)镈,則對(duì)于任意[m,n]![]() D,都存在x0∈ [m,n],使得等式f(n)-f(m)=(n-m)
D,都存在x0∈ [m,n],使得等式f(n)-f(m)=(n-m)![]() (x0)成立”,試用這一性質(zhì)證明:方程f(x)-x=0只有一個(gè)實(shí)數(shù)根;
(x0)成立”,試用這一性質(zhì)證明:方程f(x)-x=0只有一個(gè)實(shí)數(shù)根;
(Ⅲ)設(shè)x1是方程f(x)-x=0的實(shí)數(shù)根,求證:對(duì)于f(x)定義域中任意的x2,x3,當(dāng)![]() ,且
,且![]() 時(shí),
時(shí),![]() .
.
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com