題目列表(包括答案和解析)
C．選修4-4：坐標系與參數(shù)方程
在極坐標系下，已知圓O：
和直線
，
（1）求圓O和直線
的直角坐標方程；（2）當
時，求直線與圓O公共點的一個極坐標.
D．選修4-5：不等式證明選講
對于任意實數(shù)
和
，不等式
恒成立，試求實數(shù)
的取值范圍．
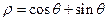和直線
，
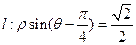的直角坐標方程；（2）當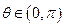
時，求直線與圓O公共點的一個極坐標.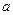
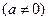和
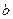，不等式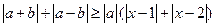
恒成立，試求實數(shù)
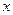的取值范圍．C
[解析] 由基本不等式，得ab≤
＝
＝
－ab，所以ab≤
，故B錯；
＋
＝
＝
≥4，故A錯；由基本不等式得
≤
＝
，即
＋
≤
，故C正確；a2＋b2＝(a＋b)2－2ab＝1－2ab≥1－2×＝，故D錯．故選C.
．定義域為R的函數(shù)
滿足
，且當
時，
，則當
時，
的最小值為（ ）
（A）
（B）
（C）
（D）
．過點
作圓
的弦，其中弦長為整數(shù)的共有 （ ）
A.16條 B. 17條 C. 32條 D. 34條
一．選擇
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
B
A
C
A
D
B
C
B
A
B
二．填空
13．
14. 0
15.100 16. ②③④
三。解答題
17．（滿分10分）
（1）
，∴
，∴
（5分）
（2）
，∴f（x）的值域為
（10分）
18．解：（1）拿每個球的概率均為
，兩球標號的和是3的倍數(shù)有下列4種情況：
（1，2），（1，5），（2，4），（3，6）每種情況的概率為：
所以所求概率為：
（6分）
（2）設拿出球的號碼是3的倍數(shù)的為事件A，則
，
，拿4次至少得2分包括2分和4分兩種情況。
，
，
（12分）
19 （滿分12分）
解法一：（Ⅰ）取BC中點O，連結AO．
為正三角形，
．……３分
連結
，在正方形
中，
分別為
的中點，
由正方形性質(zhì)知
，
．………５分
又在正方形
中，
，
平面
．……６分
（Ⅱ）設AB1與A1B交于點
，在平面
1BD中，
作
于
，連結
，由（Ⅰ）得
．
為二面角
的平面角．………９分
在
中，由等面積法可求得
，………１０分
又
，
．
所以二面角的大小為
．……１２分
解法二：（Ⅰ）取
中點
，連結
．取
中點
，以為原點，如圖建立空間直角坐標系
，則
……３分
，
．
平面．………６分
（Ⅱ）設平面
的法向量為
．
．
令
得
為平面的一個法向量．……９分
由（Ⅰ）
為平面的法向量．……１０分
．
所以二面角的大小為
．……１２分
20．（滿分12分）解：（I）
，
①
…2分
，
又
即
， ②
…4分
③
… 6分
聯(lián)立方程①②③，解得
… 7分
（II）
… 9分
令
x
（－∞，－3）
－3
（－3，1）
1
（1，+∞）
f′(x)
+
0
－
0
+
f(x)
極大
極小
故h(x)的單調(diào)增區(qū)間為（－∞，－3），（1，+∞），單調(diào)減區(qū)間為（－3，1）
21．（滿分12分）
解：（1）∵
，∴
.
∴
（
）.
∴
（）.
∴
（）.
∴
（）.
…3分
∴數(shù)列
等比，公比
，首項
，
而
，且
，∴
.
∴
.
∴
.
…6分
（2）
.
， ①
∴2
. ②
①-②得 -
，
，
…9分
∴
.
…12分
22．（滿分12分）
解：⑴設Q（x0，0），由F（-c，0）
A（0，b）知
…2分
設
，得
…4分
因為點P在橢圓上，所以
…6分
整理得2b2=
,故橢圓的離心率e=
…8分
⑵由⑴知
，
于是F（－a，0）， Q
△AQF的外接圓圓心為（a，0），半徑r=|FQ|=a
…10分
所以
，解得a=2，∴c=1，b=
，所求橢圓方程為
…12分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com