
題目列表(包括答案和解析)
已知![]() 在(-1,1)上有定義,
在(-1,1)上有定義,![]() =1,且滿足
=1,且滿足![]()
定義數列![]() :
:![]()
(1)證明:![]() 在(-1,1)上為奇函數;
在(-1,1)上為奇函數;
(2)求證{![]() }是等比數列,并求出其通項公式;
}是等比數列,并求出其通項公式;
(3)是否存在自然數m,使得對于任意
![]() 成立?若存在,求出m的最小值.。
成立?若存在,求出m的最小值.。
定義在[-1,1]上的奇函數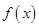 滿足
滿足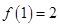 ,且當
,且當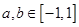 ,
,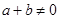 時,有
時,有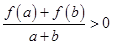 .
.
(1)試問函數f(x)的圖象上是否存在兩個不同的點A,B,使直線AB恰好與y軸垂直,若存在,求出A,B兩點的坐標;若不存在,請說明理由并加以證明.
(2)若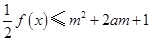 對所有
對所有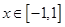 ,
,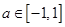 恒成立,
恒成立,
求實數m的取值范圍.
定義在[-1,1]上的奇函數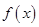 滿足
滿足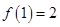 ,且當
,且當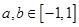 ,
,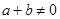 時,有
時,有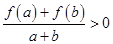 .
.
(1)試問函數f(x)的圖象上是否存在兩個不同的點A,B,使直線AB恰好與y軸垂直,若存在,求出A,B兩點的坐標;若不存在,請說明理由并加以證明.
(2)若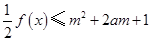 對所有
對所有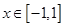 ,
,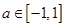 恒成立,
恒成立,
求實數m的取值范圍.
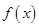 滿足
滿足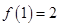 ,且當
,且當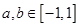 ,
,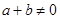 時,有
時,有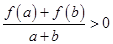 .
.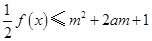 對所有
對所有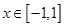 ,
,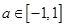 恒成立,
恒成立,是否存在這樣的k值,使函數![]() 在(1,2)上遞減,在(2,-∞)上遞增.
在(1,2)上遞減,在(2,-∞)上遞增.
一.選擇題 1B 2B 3B
二.填空題 13.3 14.  15.
15.  16.
16. 
三.解答題
17.解:由已知 所以
所以
所以 .…… 4分
.…… 4分
由 解得
解得 .
.
所以 …… 8分
…… 8分
于是 …… 10分
…… 10分
故 …… 12分
…… 12分
18.(Ⅰ)設{an}的公比為q,由a3=a1q2得  …… 2分
…… 2分
 (Ⅱ)
(Ⅱ) …… 12分
…… 12分
19.解: (1)由 知,
知,  …① ∴
…① ∴ …②…… 2分
…②…… 2分
又 恒成立,
恒成立,
有 恒成立, 故
恒成立, 故 …… 4分
…… 4分
將①式代入上式得:
 , 即
, 即 故
故 , 即
, 即 ,代入②得,
,代入②得, …… 8分
…… 8分
(2)
 即
即 ∴
∴ 解得:
解得:
 , ∴不等式的解集為
, ∴不等式的解集為 …… 12分
…… 12分
20、證(I)由a1=1,an+1= Sn(n=1,2,3,…),知a2=
Sn(n=1,2,3,…),知a2= S1=
S1= ,
,  ,∴
,∴
又an+1=Sn+1-Sn(n=1,2,3,…),則Sn+1-Sn= Sn(n=1,2,3,…),∴nSn+1=2(n+1)Sn,
Sn(n=1,2,3,…),∴nSn+1=2(n+1)Sn,
 (n=1,2,3,…).故數列{
(n=1,2,3,…).故數列{ }是首項為1,公比為2的等比數列
}是首項為1,公比為2的等比數列  …… 8分
…… 8分
證(II) 由(I)知, ,于是Sn+1=4(n+1)?
,于是Sn+1=4(n+1)? =4an(n
=4an(n )…… 12分
)…… 12分
又a2=3S1=3,則S2=a1+a2=4=
21. 解:(1) .
.
 …… 2分
…… 2分
當 時,
時,
 時,
時, , 因此
, 因此 的減區間是
的減區間是

 在區間
在區間 上是減函數
上是減函數 …… 5分
…… 5分
當 時,
時,
 時,
時, , 因此
, 因此 的減區間是
的減區間是 …… 7分
…… 7分

 在區間
在區間 上是減函數
上是減函數
綜上, 或
或 …… 8分
…… 8分
(2). 若



 在區間
在區間 上,
上,  …… 12分
…… 12分
22.解:(1)由題意和導數的幾何意義得:

由(1)得c=-a
 …… 6分
…… 6分

 …… 10分
…… 10分
 …… 14分
…… 14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com