
題目列表(包括答案和解析)
下列命題中,真命題是( )
A.直線m、n都平行于平面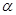 ,則m∥n ,則m∥n |
B.設(shè)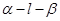 是真二面角,若直線 是真二面角,若直線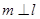 ,則 ,則 |
C.設(shè)m、n是異面直線,若m∥平面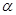 ,則n與 ,則n與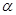 相交 相交 |
D.若直線m、n在平面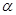 內(nèi)的射影依次是一個點和一條直線,且 內(nèi)的射影依次是一個點和一條直線,且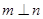 ,則 ,則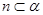 或 或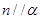 |
在下列命題中,真命題是
設(shè)α-l-β是直二面角,若直線m⊥l,則m⊥β
若直線m,n在平面α內(nèi)的射影依次是一個點和一條直線,且m⊥n,則n![]() α或n∥α
α或n∥α
直線m,n都平行于平面α,則m∥n
設(shè)m,n是異面直線,若m∥平面α,則n與α相交
下列命題中,真命題是( )
A.若直線m、n都平行于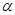 ,則
,則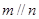
B.設(shè)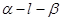 是直二面角,若直線
是直二面角,若直線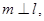 則
則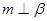
C.若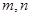 在平面
在平面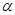 內(nèi)的射影依次是一個點和一條直線,且
內(nèi)的射影依次是一個點和一條直線,且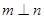 ,則
,則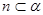 或
或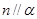
D.若直線m、n是異面直線,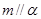 ,則n與
,則n與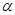 相交
相交
A.若直線m、n都平行于 ,則 ,則 |
B.設(shè) 是直二面角,若直線 是直二面角,若直線 則 則 |
C.若 在平面 在平面 內(nèi)的射影依次是一個點和一條直線,且 內(nèi)的射影依次是一個點和一條直線,且 ,則 ,則 或 或 |
D.若直線m、n是異面直線, ,則n與 ,則n與 相交 相交 |
在下列命題中,真命題是( )
A.若直線m、n都平行于平面α,則m∥n
B.設(shè)α—l—β是直二面角,若直線m⊥l,則m⊥β
C.若直線m、n在平面α內(nèi)的射影依次是一個點和一條直線,且m⊥n,則n在α內(nèi)或n與α平行
D.設(shè)m、n是異面直線,若m與平面α平行,則n與α相交
一、選擇題

二.填空題
(13)  (14)10;
(15)180;
(16)① ③④
(14)10;
(15)180;
(16)① ③④
三.解答題
(17)(本小題滿分10分)
解 :
(Ⅰ)


 函數(shù)
函數(shù)  的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為
(Ⅱ)
(18)(本小題滿分12分)
解:(I)當(dāng)


(II)由(I)得 

(19)(本小題滿分12分)
解:依題意,第四項指標(biāo)抽檢合格的概率為  其它三項指標(biāo)抽檢合格的概率均為
其它三項指標(biāo)抽檢合格的概率均為

(I)若食品監(jiān)管部門對其四項質(zhì)量指標(biāo)依次進(jìn)行嚴(yán)格的檢測,恰好在第三項指標(biāo)檢測結(jié)束
時, 能確定該食品不能上市的概率等于第一、第二項指標(biāo)中恰有一項不合格而且第三項指標(biāo)不合格的概率.

(II)該品牌的食品能上市的概率等于四項指標(biāo)都含格或第一、第二、第三項指標(biāo)中僅有
一項不合格且第四項指標(biāo)合格的概率.

(20)(本小題滿分12分)
解法1:(I)取A

 C
C CD⊥AlCl.
CD⊥AlCl.
 底面
底面  ABC是邊長為2的正三角形,
ABC是邊長為2的正三角形,
 AB=BC=2,A1B1=BlCl=2,
AB=BC=2,A1B1=BlCl=2,
 B1D⊥AlCl.
B1D⊥AlCl.
又 BlD
BlD CD=D,
CD=D, A
A
(II)  面A1ACCl⊥底面ABC,
面A1ACCl⊥底面ABC, 面AlACC1⊥A1BlC1
面AlACC1⊥A1BlC1
又B1D⊥AlC1 BID⊥面A1CCl
過點D作DE⊥A
 B1ED為所求二面角的平面角
B1ED為所求二面角的平面角
又 A
A C
C


故所求二面角B1一A .
.
解法2:(I)取AC中點O,連結(jié)BO, 
 ABC是正三角形
ABC是正三角形 BO⊥AC
BO⊥AC
又面 A1ACC1⊥底面ABC, BO⊥面A1ACC1 ,
BO⊥面A1ACC1 ,  BO⊥OA1
BO⊥OA1
又AlA=A A1O⊥AC,如圖建立空間直角坐標(biāo)系O一xyz
A1O⊥AC,如圖建立空間直角坐標(biāo)系O一xyz
 則
則 (Ⅱ)
(Ⅱ) 為平面A1B
為平面A1B
. 

故二面角B1-A
(21)(本小題滿分12分) 。
解:(I) 曲線
曲線 在點( 0,
在點( 0, )處的切線與
)處的切線與 軸平行
軸平行 
 分
分

(II)由c=0,方程  可化為
可化為 
假沒存在實數(shù)b使得此方程恰有一個實數(shù)根,

①
此方程恰有一個實根
②若b>o,則
 的變化情況如下
的變化情況如下


③若b<o(jì),則
 的變化情況如下
的變化情況如下


綜合①②③可得,實數(shù)b的取值范圍是
(22)解:,
(Ⅰ)由題意設(shè)雙曲線的標(biāo)準(zhǔn)方程為 
由已知得 

雙曲線G的標(biāo)準(zhǔn)方程為 
(Ⅱ)


化簡整理得,

www.ks5u.com
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com