
題目列表(包括答案和解析)
A.![]() B.
B.![]() C.
C.![]() D.不存在
D.不存在
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
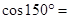 ( )
( )
A.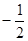 B.
B. C.
C.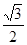 D.
D.
 =(
)
=(
)
A. B.
B. C.
C. D.
D.
一、選擇題:本大題共12小題,每小題5分,共60分
題號(hào)
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
理C
文B
C
理D
文B
C
A
B
D
C
理A
文C
B
二、填空題:本大題共4小題,每小題5分,共20分
13.第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image138.gif) 14.11 15.(理)
14.11 15.(理)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image140.gif) (文
(文第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image038.gif) )16.②④
)16.②④
三、解答題:本大題共6小題,共70分,解答應(yīng)寫(xiě)出必要的文字說(shuō)明、證明過(guò)程或演算步
驟。
17.本小題滿分10分
解:(1)由余弦定理及已知條件得,第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image142.gif) 1分
1分
∵第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image144.gif) 3分
3分
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image146.gif) 5分
5分
(2)由正弦定理及已知條件得,b=
聯(lián)立方程組第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image148.gif) 9分
9分
∴△ABC的周長(zhǎng)為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image150.gif) 10分
10分
18.本小題滿分12分
解:(1)記“該參賽者恰好連對(duì)一條線”為事件A。
則第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image152.gif) (理)4分(文)6分
(理)4分(文)6分
(2)(理科)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image106.gif) 的所有可能取值為-4、0、4、12 5分
的所有可能取值為-4、0、4、12 5分
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image155.gif)
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image157.gif) 9分
9分
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image106.gif) 的分布列為
的分布列為
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image106.gif)
-4
0
4
12
3/8
1/3
1/4
1/24
E第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image106.gif) =
=第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image160.gif) 12分
12分
(文科)該參賽者所有可能得分為-4、0、4、12. 7分
得0分的概率為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image162.gif) 8分
8分
得4分的概率為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image164.gif) 9分
9分
得12分的概率為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image166.gif) 10分
10分
∴該參賽者得分為非負(fù)數(shù)的概率為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image168.gif) 12分
12分
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image170.jpg) 19.本小題滿分12分
19.本小題滿分12分
解:(1)取AB的中點(diǎn)G,連接CG,F(xiàn)G,
則FG∥BE,且FG=第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image072.gif) BE,
BE,
∴FG∥CD,且FG=CD,2分
∴四邊形FGCD是平行四邊形,
∴DF∥CG,
又∵CF第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image172.gif) 平面ABC,
平面ABC,
∴DF∥平面ABC, 6分
(2)解法一:設(shè)A到平面BDF的距離為h,
由第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image174.gif) 8分
8分
在△BDF中,第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image176.gif)
且CB=2,∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image178.gif) 10分
10分
設(shè)AB于平面BDF所成的角為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image180.gif) ,則
,則第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image182.gif)
故AB與平面BDF所成的角為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image184.gif) 12分
12分
解法二:以點(diǎn)B為原點(diǎn),BA、BC、BE所在的直線分別為x、y、z軸,建立空間直角
坐標(biāo)系,則
B(0,0,0),A(2,0,0),C(0,2,0),D(0,2,1)E(0,0,2),
F(1,0,1)。…………………………………………………………………………… 8分
∴ 第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image186.gif) =(0,2,1),
=(0,2,1),第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image188.gif) =(1,-2,0)…………………………………………… 8分
=(1,-2,0)…………………………………………… 8分
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image190.jpg) 設(shè)平面BDF的一個(gè)法向量為n=(2,a,b),
設(shè)平面BDF的一個(gè)法向量為n=(2,a,b),
∵ n⊥第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image188.gif) ,n⊥
,n⊥第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image186.gif) ,∴
,∴ 第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image192.gif)
即第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image194.gif) 解得
解得第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image196.gif)
∴ n=(2,1,-2)……………………………10分
又設(shè)AB與平面BDF所成的角為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image180.gif) ,則法線n與
,則法線n與第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image199.gif) 所成的角為
所成的角為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image201.gif) ,
,
∴cos(第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image201.gif) )=
)=第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image204.gif) =
=第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image206.gif) =
=第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image208.gif) ,
,
即sin第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image210.gif) ,故AB與平面BDF所成的角為arcsin
,故AB與平面BDF所成的角為arcsin第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image208.gif) .…………………………… 12分
.…………………………… 12分
20.本小題滿分12分
解:(1)∵第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image213.gif) -
-第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image215.gif) =0,因?yàn)椋?sub>
=0,因?yàn)椋?sub>第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image217.gif) )(
)(第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image219.gif) )=0,
)=0,
∵數(shù)列第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image221.gif) 的各項(xiàng)均為正數(shù),∴
的各項(xiàng)均為正數(shù),∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image217.gif) >0,∴
>0,∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image219.gif) =0,
=0,
即第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image224.gif) 所以數(shù)列
所以數(shù)列第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image221.gif) 是以2為公比的等比數(shù)列…………………………………3分
是以2為公比的等比數(shù)列…………………………………3分
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image226.gif) 是
是第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image228.gif) 的等差中項(xiàng),∴
的等差中項(xiàng),∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image230.gif) ,∴
,∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image232.gif)
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image234.gif) ∴數(shù)列
∴數(shù)列第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image221.gif) 的通項(xiàng)公式
的通項(xiàng)公式第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image236.gif) ……………………………………………… 6分
……………………………………………… 6分
(2)由(1)及第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image238.gif) log
log第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image240.gif)
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image242.gif) 得,
得,第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image244.gif) ,………………………………… 8分
,………………………………… 8分
∵第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image246.gif) …
…第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image248.gif)
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image250.gif) -…-
-…-第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image252.gif) ①
①
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image254.gif) -…-
-…-第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image256.gif) ②
②
②-①得,第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image258.gif) +…+
+…+第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image260.gif)
=第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image262.gif) ……………………… (理)10分(文)12分
……………………… (理)10分(文)12分
要使第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image264.gif) >50成立,只需
>50成立,只需 第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image266.gif) >50成立,即
>50成立,即第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image260.gif) >52,n
>52,n第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image269.gif)
∴使第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image264.gif) >50成立的正整數(shù)n的最小值為5。………………………(理)12分
>50成立的正整數(shù)n的最小值為5。………………………(理)12分
21.本小題滿分12分
解:(1)由第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image271.gif) 得(
得(第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image273.gif) )
)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image275.gif) ………………1分
………………1分
當(dāng)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image277.gif) 時(shí)直線與雙曲線無(wú)交點(diǎn),這和直線與雙曲線恒有公共點(diǎn)矛盾,
時(shí)直線與雙曲線無(wú)交點(diǎn),這和直線與雙曲線恒有公共點(diǎn)矛盾,
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image279.gif) ≠2,e≠
≠2,e≠第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image281.gif) …………………………………………………………………………2分
…………………………………………………………………………2分
當(dāng)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image279.gif) ≠2時(shí),
≠2時(shí),第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image284.gif) =
=第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image286.gif) 恒成立,
恒成立,
即第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image288.gif) 恒成立,
恒成立,
∵第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image279.gif) >0,∴
>0,∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image290.gif) ,∴
,∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image279.gif)
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image292.gif) ,……………………………………3分
,……………………………………3分
∵第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image294.gif)
∵(第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image296.gif) )
)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image298.gif) =2,∴
=2,∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image300.gif) ∴
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image302.gif)
綜上知第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image304.gif) ………………………………………………………………………6分
………………………………………………………………………6分
(Ⅱ)設(shè)F(c,0),則l:y=x-c,將x=y+c代入雙曲線方程,得
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image306.gif)
整理得第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image308.gif) …………………………………………7分
…………………………………………7分
設(shè)兩交點(diǎn)為P(第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image310.gif) ),Q
),Q第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image312.gif) ,則
,則第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image314.gif)
∵第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image316.gif) =
=第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image318.gif) ∴
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image320.gif) ……………………………………………………………8分
……………………………………………………………8分
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image322.gif) 消去
消去第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image324.gif) 得
得
第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image326.gif) ………………………………………………………………10分
………………………………………………………………10分
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image279.gif) >0且
>0且第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image329.gif) ∴
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image331.gif) ∴
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image333.gif)
∴所求雙曲線C的方程為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image335.gif) ………………………………………………12分
………………………………………………12分
22.本小題滿分12分
(理科)解:(1)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image337.gif) ……………………………………………2分
……………………………………………2分
∵x=0時(shí),第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image088.gif) 取極值0,∴
取極值0,∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image340.gif) ………………………………………………3分
………………………………………………3分
解得a=1,b=0.經(jīng)檢驗(yàn)a=1,b=0符合題意。………………………………………………4分
(2)由a=1,b=0知第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image342.gif) 由
由第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image344.gif)
得第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image346.gif)
令第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image348.gif) 則
則第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image130.gif) 在
在第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image351.gif) 上恰有兩個(gè)不同的實(shí)數(shù)
上恰有兩個(gè)不同的實(shí)數(shù)
根等價(jià)于第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image353.gif) 在
在第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image351.gif) 上恰有兩個(gè)不同實(shí)數(shù)根。
上恰有兩個(gè)不同實(shí)數(shù)根。
當(dāng)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image356.gif) 時(shí),
時(shí),第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image358.gif) <0,于是
<0,于是第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image358.gif) 在(0,1)上單調(diào)遞減;
在(0,1)上單調(diào)遞減;
當(dāng)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image361.gif) 時(shí),
時(shí),第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image358.gif) >0,于是
>0,于是第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image358.gif) 在(1,2)上單調(diào)遞增。……………………7分
在(1,2)上單調(diào)遞增。……………………7分
依題意有第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image364.gif) <0,∴
<0,∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image366.gif) …………………8分
…………………8分
(3)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image368.gif) 的定義域?yàn)?sub>
的定義域?yàn)?sub>第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image370.gif) >
>第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image372.gif) ,
,
由(1)知第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image374.gif)
當(dāng)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image376.gif) 單調(diào)遞減。
單調(diào)遞減。
當(dāng)x>0時(shí),第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image088.gif) >0,
>0,第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image088.gif) 單調(diào)遞增。
單調(diào)遞增。
∴f(0)為第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image088.gif) 在(-1,+∞)上的最小值,∴
在(-1,+∞)上的最小值,∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image088.gif) ≥f(0)
≥f(0)
又f(0)=0,故第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image378.gif) (當(dāng)且僅當(dāng)x=0,等號(hào)成立) 10分
(當(dāng)且僅當(dāng)x=0,等號(hào)成立) 10分
對(duì)任意正整數(shù)n,取第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image380.gif)
故第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image382.gif)
=第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image384.gif) 12分
12分
(文科)解:(1)∵第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image386.gif) 1分
1分
依題意有第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image388.gif) 3分
3分
解得第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image390.gif) 4分
4分
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image392.gif) 5分
5分
(2)∵第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image394.gif) ,依題意x1、x2是方程
,依題意x1、x2是方程第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image088.gif) =0的兩個(gè)根,
=0的兩個(gè)根,
由第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image136.gif) ∴
∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image397.gif) 7分
7分
設(shè)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image399.gif)
由第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image401.gif) 9分
9分
即函數(shù)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image403.gif) 在區(qū)間(0,4)上是增函數(shù),在區(qū)間(4,6)上是減函數(shù)
在區(qū)間(0,4)上是增函數(shù),在區(qū)間(4,6)上是減函數(shù)
當(dāng)第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image405.gif) 時(shí),
時(shí),第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image403.gif) 有極大值為96,∴
有極大值為96,∴第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image403.gif) 在(0,6)上的最大值是96 10分
在(0,6)上的最大值是96 10分
∴b的最大值為4第二次高考診斷%20數(shù)學(xué)(文理科)word版.files/image407.gif) 12分
12分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com