
題目列表(包括答案和解析)
(本題滿分12分)![]() 學(xué)科網(wǎng)某地區(qū)試行高考考試改革:在高三學(xué)年中舉行5次統(tǒng)一測(cè)試,學(xué)生如果通過(guò)其中2次測(cè)試即可獲得足夠?qū)W分升上大學(xué)繼續(xù)學(xué)習(xí),不用參加其余的測(cè)試,而每個(gè)學(xué)生最多也只能參加5次測(cè)試. 假設(shè)某學(xué)生每次通過(guò)測(cè)試的概率都是
學(xué)科網(wǎng)某地區(qū)試行高考考試改革:在高三學(xué)年中舉行5次統(tǒng)一測(cè)試,學(xué)生如果通過(guò)其中2次測(cè)試即可獲得足夠?qū)W分升上大學(xué)繼續(xù)學(xué)習(xí),不用參加其余的測(cè)試,而每個(gè)學(xué)生最多也只能參加5次測(cè)試. 假設(shè)某學(xué)生每次通過(guò)測(cè)試的概率都是![]() ,每次測(cè)試通過(guò)與否互相獨(dú)立. 規(guī)定:若前4次都沒(méi)有通過(guò)測(cè)試,則第5次不能參加測(cè)試.
,每次測(cè)試通過(guò)與否互相獨(dú)立. 規(guī)定:若前4次都沒(méi)有通過(guò)測(cè)試,則第5次不能參加測(cè)試.![]() 學(xué)科網(wǎng)(1)求該學(xué)生恰好經(jīng)過(guò)4次測(cè)試考上大學(xué)的概率;
學(xué)科網(wǎng)(1)求該學(xué)生恰好經(jīng)過(guò)4次測(cè)試考上大學(xué)的概率;![]() 學(xué)科網(wǎng)(2) 求該學(xué)生考上大學(xué)的概率.
學(xué)科網(wǎng)(2) 求該學(xué)生考上大學(xué)的概率.![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(本題滿分12分)[來(lái)源:學(xué)科網(wǎng)]
某校積極響應(yīng)《全面健身?xiàng)l例》,把周五下午5:0![]() 0~6:00定為職工活動(dòng)時(shí)間,并成立了行政和教師兩支籃球隊(duì),但由于工作性質(zhì)所限,每月(假設(shè)為4周)每支球隊(duì)只能組織兩次活動(dòng),且兩支球隊(duì)的活動(dòng)時(shí)間是相互獨(dú)立的。
0~6:00定為職工活動(dòng)時(shí)間,并成立了行政和教師兩支籃球隊(duì),但由于工作性質(zhì)所限,每月(假設(shè)為4周)每支球隊(duì)只能組織兩次活動(dòng),且兩支球隊(duì)的活動(dòng)時(shí)間是相互獨(dú)立的。
(1)求這兩![]() 支球隊(duì)每月兩次都在同一時(shí)間活動(dòng)的頻率;
支球隊(duì)每月兩次都在同一時(shí)間活動(dòng)的頻率;
(2)設(shè)這兩支球隊(duì)每月能同時(shí)活動(dòng)的次數(shù)為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望。
的分布列和數(shù)學(xué)期望。
(本題滿分12分)
為預(yù)防![]() 病毒暴發(fā),某生物技術(shù)公司研制出一種新流感疫苗,為測(cè)試該疫苗的有效性(若疫苗有效的概率小于90%,則認(rèn)為測(cè)試沒(méi)
病毒暴發(fā),某生物技術(shù)公司研制出一種新流感疫苗,為測(cè)試該疫苗的有效性(若疫苗有效的概率小于90%,則認(rèn)為測(cè)試沒(méi)![]() 有通過(guò)),公司選定2000個(gè)流感樣本分成三組,測(cè)試結(jié)果如下表:
有通過(guò)),公司選定2000個(gè)流感樣本分成三組,測(cè)試結(jié)果如下表:
| A組 | B組 | C組[來(lái)源:學(xué)科網(wǎng)ZXXK] | |
| 疫苗有效 | 673 |
|
|
| 疫苗無(wú)效 | 77 | 90[來(lái)源:Z&xx&k.Com] |
|
已知在全體樣本中隨機(jī)抽取1個(gè),抽到B組疫苗有效的概率是0.33.
(1)求![]() 的值;
的值;
(2)現(xiàn)用分層抽樣的方法在全體樣本中抽取360個(gè)測(cè)試結(jié)果,問(wèn)應(yīng)在C組抽取多少個(gè)?
(3)已知![]() ,求不能通過(guò)測(cè)試的概率.
,求不能通過(guò)測(cè)試的概率.
(本題滿分12分) 已知函數(shù)![]()
![]() 學(xué)科網(wǎng)1)若函數(shù)
學(xué)科網(wǎng)1)若函數(shù)![]() ;
;
(2)設(shè)![]() ,若p是q的充分條件,求實(shí)數(shù)m的取值范圍.
,若p是q的充分條件,求實(shí)數(shù)m的取值范圍.![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(本題滿分12分)
如圖,四棱錐P-ABCD的側(cè)面PAD垂直于底面ABCD,∠ADC=∠BCD= ,PA=PD=AD=2BC=2,CD
,PA=PD=AD=2BC=2,CD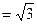 ,M在棱PC上,N是AD的中點(diǎn),二面角M-BN-C為
,M在棱PC上,N是AD的中點(diǎn),二面角M-BN-C為 .
.
(1)求 的值;
的值;
(2)求直線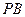 與平面BMN所成角的大小.[來(lái)源:學(xué)科網(wǎng)
與平面BMN所成角的大小.[來(lái)源:學(xué)科網(wǎng) ZXXK]
ZXXK]
一. 選擇題 : (本大題共10小題, 每小題5分, 共50分)
ABDCC DDBCB
二.填空題: (本大題共5小題, 每小題5分, 共25分)
11.1680 12.5
13.-1 14.考第一次考試文科數(shù)學(xué)試卷.files/image244.gif) 15.
15.考第一次考試文科數(shù)學(xué)試卷.files/image246.gif)
三. 解答題: (本大題共6小題, 共75分)
16.(本小題滿分12分)
解:(1)f(x)考第一次考試文科數(shù)學(xué)試卷.files/image247.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image249.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image251.gif) ......3分
......3分
考第一次考試文科數(shù)學(xué)試卷.files/image253.gif) ……4分
……4分
令考第一次考試文科數(shù)學(xué)試卷.files/image255.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image257.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image259.gif) 的單調(diào)區(qū)間為
的單調(diào)區(qū)間為考第一次考試文科數(shù)學(xué)試卷.files/image261.gif) ,k∈Z ...............6分
,k∈Z ...............6分
(2)由考第一次考試文科數(shù)學(xué)試卷.files/image263.gif) 得
得考第一次考試文科數(shù)學(xué)試卷.files/image265.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image267.gif) ......7分
......7分
又考第一次考試文科數(shù)學(xué)試卷.files/image269.gif) 為
為考第一次考試文科數(shù)學(xué)試卷.files/image080.gif) 的內(nèi)角
的內(nèi)角 考第一次考試文科數(shù)學(xué)試卷.files/image272.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image274.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image276.gif) .....9分
.....9分
考第一次考試文科數(shù)學(xué)試卷.files/image278.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image280.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image282.gif) .......11分
.......11分
考第一次考試文科數(shù)學(xué)試卷.files/image284.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image286.gif) ......12分
......12分
17.(本小題滿分12分)
解:(1)考第一次考試文科數(shù)學(xué)試卷.files/image288.gif) .......5分
.......5分
考第一次考試文科數(shù)學(xué)試卷.files/image290.gif) .......12分
.......12分
18.(本題滿分12分)
解法一:
(1)在棱考第一次考試文科數(shù)學(xué)試卷.files/image292.gif) 取三等分點(diǎn)
取三等分點(diǎn)考第一次考試文科數(shù)學(xué)試卷.files/image294.gif) ,使
,使考第一次考試文科數(shù)學(xué)試卷.files/image296.gif) ,則
,則考第一次考試文科數(shù)學(xué)試卷.files/image298.gif) ,由
,由考第一次考試文科數(shù)學(xué)試卷.files/image300.gif) ⊥平面
⊥平面考第一次考試文科數(shù)學(xué)試卷.files/image155.gif) ,
,
得考第一次考試文科數(shù)學(xué)試卷.files/image303.gif) ⊥平面
⊥平面考第一次考試文科數(shù)學(xué)試卷.files/image155.gif) 。過(guò)點(diǎn)
。過(guò)點(diǎn)考第一次考試文科數(shù)學(xué)試卷.files/image305.gif) 作
作考第一次考試文科數(shù)學(xué)試卷.files/image307.gif) 于
于考第一次考試文科數(shù)學(xué)試卷.files/image309.gif) ,連結(jié)
,連結(jié)考第一次考試文科數(shù)學(xué)試卷.files/image311.gif) ,
,
考第一次考試文科數(shù)學(xué)試卷.files/image312.gif) 則
則考第一次考試文科數(shù)學(xué)試卷.files/image314.gif) ,
,考第一次考試文科數(shù)學(xué)試卷.files/image316.gif) 為所求二面角
為所求二面角考第一次考試文科數(shù)學(xué)試卷.files/image318.gif) 的平面角.
的平面角.
在考第一次考試文科數(shù)學(xué)試卷.files/image320.gif) 中,
中,考第一次考試文科數(shù)學(xué)試卷.files/image322.gif) ,
,
考第一次考試文科數(shù)學(xué)試卷.files/image324.gif) ,
,考第一次考試文科數(shù)學(xué)試卷.files/image326.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image327.gif) 所以,二面角
所以,二面角考第一次考試文科數(shù)學(xué)試卷.files/image318.gif) 的余弦值為
的余弦值為考第一次考試文科數(shù)學(xué)試卷.files/image329.gif) ......6分
......6分
(2)因?yàn)?sub>考第一次考試文科數(shù)學(xué)試卷.files/image331.gif) ,所以點(diǎn)
,所以點(diǎn)考第一次考試文科數(shù)學(xué)試卷.files/image333.gif) 到平面
到平面考第一次考試文科數(shù)學(xué)試卷.files/image335.gif) 的距離等于
的距離等于
考第一次考試文科數(shù)學(xué)試卷.files/image337.gif) 到平面
到平面考第一次考試文科數(shù)學(xué)試卷.files/image335.gif) 的距離,
的距離,考第一次考試文科數(shù)學(xué)試卷.files/image300.gif) ⊥平面
⊥平面考第一次考試文科數(shù)學(xué)試卷.files/image155.gif) ,
,
過(guò)點(diǎn)考第一次考試文科數(shù)學(xué)試卷.files/image337.gif) 作
作考第一次考試文科數(shù)學(xué)試卷.files/image340.gif) 于
于考第一次考試文科數(shù)學(xué)試卷.files/image342.gif) ,連結(jié)
,連結(jié)考第一次考試文科數(shù)學(xué)試卷.files/image344.gif) ,則
,則考第一次考試文科數(shù)學(xué)試卷.files/image346.gif) ,
,
考第一次考試文科數(shù)學(xué)試卷.files/image348.gif) ⊥平面
⊥平面考第一次考試文科數(shù)學(xué)試卷.files/image350.gif) ,過(guò)點(diǎn)
,過(guò)點(diǎn)考第一次考試文科數(shù)學(xué)試卷.files/image337.gif) 作
作考第一次考試文科數(shù)學(xué)試卷.files/image352.gif) 于
于考第一次考試文科數(shù)學(xué)試卷.files/image354.gif) ,
,
則考第一次考試文科數(shù)學(xué)試卷.files/image356.gif) ,
,考第一次考試文科數(shù)學(xué)試卷.files/image358.gif) 為所求距離,
為所求距離,
考第一次考試文科數(shù)學(xué)試卷.files/image359.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image361.gif)
所以,求點(diǎn)考第一次考試文科數(shù)學(xué)試卷.files/image333.gif) 到平面
到平面考第一次考試文科數(shù)學(xué)試卷.files/image335.gif) 的距離為
的距離為考第一次考試文科數(shù)學(xué)試卷.files/image363.gif) ......12分
......12分
解法二:
證明:(1)建立如圖所示的直角坐標(biāo)系,
則A(0,0,0)、D(0,3,0)、P(0,0,3)、
B(4,0,0)、C(4,3,0), 由已知得考第一次考試文科數(shù)學(xué)試卷.files/image365.gif) ,
,
得考第一次考試文科數(shù)學(xué)試卷.files/image367.gif) .
.
設(shè)平面QAC的法向量為考第一次考試文科數(shù)學(xué)試卷.files/image369.gif) ,則
,則考第一次考試文科數(shù)學(xué)試卷.files/image371.gif) ,
,
即考第一次考試文科數(shù)學(xué)試卷.files/image373.gif) ∴
∴考第一次考試文科數(shù)學(xué)試卷.files/image375.gif) ,令
,令考第一次考試文科數(shù)學(xué)試卷.files/image377.gif) ,得到平面QAC的一個(gè)法向量為
,得到平面QAC的一個(gè)法向量為考第一次考試文科數(shù)學(xué)試卷.files/image379.gif)
∵PA⊥平面ABCD,∴考第一次考試文科數(shù)學(xué)試卷.files/image381.gif) 為平面ABCD的法向量.
為平面ABCD的法向量.
設(shè)二面角P―CD―B的大小為q,依題意可得考第一次考試文科數(shù)學(xué)試卷.files/image383.gif) .....6分
.....6分
(2)由(1)得考第一次考試文科數(shù)學(xué)試卷.files/image385.gif)
設(shè)平面PBD的法向量為考第一次考試文科數(shù)學(xué)試卷.files/image387.gif) ,則
,則考第一次考試文科數(shù)學(xué)試卷.files/image389.gif) ,
,
即考第一次考試文科數(shù)學(xué)試卷.files/image391.gif) ,∴令
,∴令考第一次考試文科數(shù)學(xué)試卷.files/image393.gif) ,得到平面QAC的一個(gè)為法向量為
,得到平面QAC的一個(gè)為法向量為考第一次考試文科數(shù)學(xué)試卷.files/image395.gif)
19. (本小題滿分13分)
(1)解:當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image206.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image402.gif) 時(shí),
時(shí),考第一次考試文科數(shù)學(xué)試卷.files/image404.gif) ,………………………………①
,………………………………①
則當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image406.gif) ,
, 考第一次考試文科數(shù)學(xué)試卷.files/image206.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image402.gif) 時(shí),
時(shí),考第一次考試文科數(shù)學(xué)試卷.files/image408.gif) ………………②
………………②
①-②,得考第一次考試文科數(shù)學(xué)試卷.files/image410.gif) ,即
,即考第一次考試文科數(shù)學(xué)試卷.files/image412.gif)
∴考第一次考試文科數(shù)學(xué)試卷.files/image414.gif) ,∴
,∴考第一次考試文科數(shù)學(xué)試卷.files/image416.gif) ,當(dāng)
,當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image418.gif) 時(shí),
時(shí),考第一次考試文科數(shù)學(xué)試卷.files/image420.gif) ,則
,則考第一次考試文科數(shù)學(xué)試卷.files/image422.gif) .
.
∴考第一次考試文科數(shù)學(xué)試卷.files/image424.gif) 是以
是以考第一次考試文科數(shù)學(xué)試卷.files/image426.gif) 為首項(xiàng),
為首項(xiàng),考第一次考試文科數(shù)學(xué)試卷.files/image428.gif) 為公比的等比數(shù)列,∴
為公比的等比數(shù)列,∴考第一次考試文科數(shù)學(xué)試卷.files/image430.gif) ,
,
∴考第一次考試文科數(shù)學(xué)試卷.files/image432.gif) ………………………6分
………………………6分
(2)證明:考第一次考試文科數(shù)學(xué)試卷.files/image434.gif) .
.
∴考第一次考試文科數(shù)學(xué)試卷.files/image436.gif) , 則
, 則考第一次考試文科數(shù)學(xué)試卷.files/image438.gif) ,…………③
,…………③
考第一次考試文科數(shù)學(xué)試卷.files/image440.gif) …………………………④
…………………………④
③-④,得考第一次考試文科數(shù)學(xué)試卷.files/image442.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image444.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image446.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image448.gif) ∴
∴考第一次考試文科數(shù)學(xué)試卷.files/image450.gif) .
.
當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image406.gif) 時(shí),
時(shí),考第一次考試文科數(shù)學(xué)試卷.files/image453.gif) , ∴
, ∴考第一次考試文科數(shù)學(xué)試卷.files/image455.gif) 為遞增數(shù)列,
為遞增數(shù)列,
∴考第一次考試文科數(shù)學(xué)試卷.files/image457.gif) ........13分
........13分
考第一次考試文科數(shù)學(xué)試卷.files/image459.jpg) 20.(本小題滿分13分)
20.(本小題滿分13分)
解法一:
(1)設(shè)橢圓方程為考第一次考試文科數(shù)學(xué)試卷.files/image461.gif) (a>b>0),由已知c=1,
(a>b>0),由已知c=1,
又考第一次考試文科數(shù)學(xué)試卷.files/image463.gif) .
.
所以a=考第一次考試文科數(shù)學(xué)試卷.files/image465.gif) ,b2=a2-c2=1,
,b2=a2-c2=1,
橢圓C的方程是x2+ 考第一次考試文科數(shù)學(xué)試卷.files/image467.gif) =1. .......4分
=1. .......4分
(2)若直線l與x軸重合,則以AB為直徑的圓是x2+y2=1,
若直線l垂直于x軸,則以AB為直徑的圓是(x+考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) )2+y2=
)2+y2=考第一次考試文科數(shù)學(xué)試卷.files/image471.gif) .
.
由考第一次考試文科數(shù)學(xué)試卷.files/image473.gif) 解得
解得考第一次考試文科數(shù)學(xué)試卷.files/image475.gif) 即兩圓相切于點(diǎn)(1,0).
即兩圓相切于點(diǎn)(1,0).
因此所求的點(diǎn)T如果存在,只能是(1,0). 事實(shí)上,點(diǎn)T(1,0)就是所求的點(diǎn)........6分
證明如下:
當(dāng)直線l垂直于x軸時(shí),以AB為直徑的圓過(guò)點(diǎn)T(1,0).
若直線l不垂直于x軸,可設(shè)直線l:y=k(x+考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) ).
).
由考第一次考試文科數(shù)學(xué)試卷.files/image478.gif) 即(k2+2)x2+
即(k2+2)x2+考第一次考試文科數(shù)學(xué)試卷.files/image480.gif) k2x+
k2x+考第一次考試文科數(shù)學(xué)試卷.files/image482.gif) k2-2=0.記點(diǎn)A(x1,y1),B(x2,y2),則
k2-2=0.記點(diǎn)A(x1,y1),B(x2,y2),則考第一次考試文科數(shù)學(xué)試卷.files/image484.gif)
由考第一次考試文科數(shù)學(xué)試卷.files/image486.gif) =(x1-1, y1),
=(x1-1, y1), 考第一次考試文科數(shù)學(xué)試卷.files/image488.gif) =(x2-1, y2),
=(x2-1, y2), 考第一次考試文科數(shù)學(xué)試卷.files/image490.gif) =(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+
=(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) )(x2+
)(x2+考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) )
)
=(k2+1)x1x2+(考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) k2-1)(x1+x2)+
k2-1)(x1+x2)+考第一次考試文科數(shù)學(xué)試卷.files/image482.gif) k2+1=(k2+1)
k2+1=(k2+1) 考第一次考試文科數(shù)學(xué)試卷.files/image496.gif) +(
+(考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) k2-1)
k2-1) 考第一次考試文科數(shù)學(xué)試卷.files/image499.gif) +
+ 考第一次考試文科數(shù)學(xué)試卷.files/image501.gif) +1=0,
+1=0,
所以TA⊥TB,即以AB為直徑的圓恒過(guò)點(diǎn)T(1,0).故在坐標(biāo)平面上存在一個(gè)定點(diǎn)T(1,0)滿足條件.......13分
解法二:
(1)由已知c=1,設(shè)橢圓C的方程是考第一次考試文科數(shù)學(xué)試卷.files/image503.gif) (a>1).
(a>1).
因?yàn)辄c(diǎn)P在橢圓C上,所以考第一次考試文科數(shù)學(xué)試卷.files/image505.gif) ,解得a2=2,所以橢圓C的方程是:
,解得a2=2,所以橢圓C的方程是:考第一次考試文科數(shù)學(xué)試卷.files/image507.gif) .
.
.......4分
(2)假設(shè)存在定點(diǎn)T(u,v)滿足條件.同解法一得(k2+2)x2+考第一次考試文科數(shù)學(xué)試卷.files/image480.gif) k2x+
k2x+考第一次考試文科數(shù)學(xué)試卷.files/image482.gif) k2-2=0.
k2-2=0.
記點(diǎn)A(x1,y1),B(x2,y2),則考第一次考試文科數(shù)學(xué)試卷.files/image511.gif)
又因?yàn)?sub>考第一次考試文科數(shù)學(xué)試卷.files/image486.gif) =(x1-u, y1-v),
=(x1-u, y1-v), 考第一次考試文科數(shù)學(xué)試卷.files/image488.gif) =(x2-u, y2-v),及y1=k(x1+
=(x2-u, y2-v),及y1=k(x1+考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) ),y2=k(x2+
),y2=k(x2+考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) ).
).
所以考第一次考試文科數(shù)學(xué)試卷.files/image517.gif) =(x1-u)(x2-u)+(y1-v)(y2-v)
=(x1-u)(x2-u)+(y1-v)(y2-v)
=(k2+1)x1x2+(考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) k2-u-kv)(x1+x2)+
k2-u-kv)(x1+x2)+考第一次考試文科數(shù)學(xué)試卷.files/image482.gif) k2-
k2-考第一次考試文科數(shù)學(xué)試卷.files/image521.gif) v+u2+v2
v+u2+v2
=考第一次考試文科數(shù)學(xué)試卷.files/image523.gif)
當(dāng)且僅當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image486.gif) ?
?考第一次考試文科數(shù)學(xué)試卷.files/image488.gif) =0恒成立時(shí),以AB為直徑的圓恒過(guò)點(diǎn)T.
=0恒成立時(shí),以AB為直徑的圓恒過(guò)點(diǎn)T.
考第一次考試文科數(shù)學(xué)試卷.files/image486.gif) ?
?考第一次考試文科數(shù)學(xué)試卷.files/image488.gif) =0恒成立等價(jià)于
=0恒成立等價(jià)于考第一次考試文科數(shù)學(xué)試卷.files/image529.gif) 解得u=1,v=0.
解得u=1,v=0.
此時(shí),以AB為直徑的圓恒過(guò)定點(diǎn)T(1,0). 當(dāng)直線l垂直于x軸時(shí),以AB為直徑的圓考第一次考試文科數(shù)學(xué)試卷.files/image531.gif) 亦過(guò)點(diǎn)T(1,0).所以在坐標(biāo)平面上存在一個(gè)定點(diǎn)T(1,O)滿足條件
亦過(guò)點(diǎn)T(1,0).所以在坐標(biāo)平面上存在一個(gè)定點(diǎn)T(1,O)滿足條件
........13分
解法三:
(1)同解法一或解法二........4分
(2)設(shè)坐標(biāo)平面上存在一個(gè)定點(diǎn)T滿足條件,根據(jù)直線過(guò)x軸上的定點(diǎn)S及橢圓的對(duì)稱性,所求的點(diǎn)T如果存在,只能在x軸上,設(shè)T(t,O).
同解法一得考第一次考試文科數(shù)學(xué)試卷.files/image533.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image535.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image486.gif) =(x1-t,y1),
=(x1-t,y1),考第一次考試文科數(shù)學(xué)試卷.files/image488.gif) =(x2-t,y2)
=(x2-t,y2)
考第一次考試文科數(shù)學(xué)試卷.files/image539.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image540.gif) =(x1-t)(x2-t)+y1y2=(x1-t)(x2-t)+k2(x1+
=(x1-t)(x2-t)+y1y2=(x1-t)(x2-t)+k2(x1+考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) )(x2+
)(x2+考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) )
)
=(k2+1)x1x2+(考第一次考試文科數(shù)學(xué)試卷.files/image469.gif) k2-t)(x1+x2)+
k2-t)(x1+x2)+考第一次考試文科數(shù)學(xué)試卷.files/image482.gif) k2+t2=
k2+t2=考第一次考試文科數(shù)學(xué)試卷.files/image546.gif)
當(dāng)且僅當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image486.gif) ?
?考第一次考試文科數(shù)學(xué)試卷.files/image488.gif) =O恒成立時(shí),以AB為直徑的圓恒過(guò)點(diǎn)T.
=O恒成立時(shí),以AB為直徑的圓恒過(guò)點(diǎn)T.
考第一次考試文科數(shù)學(xué)試卷.files/image486.gif) ?
?考第一次考試文科數(shù)學(xué)試卷.files/image488.gif) =O恒成立等價(jià)于
=O恒成立等價(jià)于考第一次考試文科數(shù)學(xué)試卷.files/image552.gif) 解得t=1.所以當(dāng)t=1時(shí),以AB為直徑的圓恒過(guò)點(diǎn)T.
解得t=1.所以當(dāng)t=1時(shí),以AB為直徑的圓恒過(guò)點(diǎn)T.
當(dāng)直線l垂直于x軸時(shí),以AB為直徑的圓考第一次考試文科數(shù)學(xué)試卷.files/image531.gif) 亦過(guò)點(diǎn)T(1,O).
亦過(guò)點(diǎn)T(1,O).
所以在坐標(biāo)平面上存在一個(gè)定點(diǎn)T(1,O)滿足條件........13分
21. (本小題滿分13分)
解:(1)由題意
考第一次考試文科數(shù)學(xué)試卷.files/image555.gif) …………………………1分
…………………………1分
考第一次考試文科數(shù)學(xué)試卷.files/image535.gif) 當(dāng)
當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image231.gif) 時(shí),
時(shí),考第一次考試文科數(shù)學(xué)試卷.files/image180.gif) 取得極值,
取得極值, 考第一次考試文科數(shù)學(xué)試卷.files/image539.gif) 所以
所以 考第一次考試文科數(shù)學(xué)試卷.files/image561.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image563.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image539.gif) 即
即 考第一次考試文科數(shù)學(xué)試卷.files/image566.gif) …………………3分
…………………3分
此時(shí)當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image568.gif) 時(shí),
時(shí),考第一次考試文科數(shù)學(xué)試卷.files/image570.gif) ,當(dāng)
,當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image572.gif) 時(shí),
時(shí),考第一次考試文科數(shù)學(xué)試卷.files/image574.gif) ,
,
考第一次考試文科數(shù)學(xué)試卷.files/image235.gif) 是函數(shù)
是函數(shù)考第一次考試文科數(shù)學(xué)試卷.files/image180.gif) 的最小值。 ………………………5分
的最小值。 ………………………5分
(2)設(shè)考第一次考試文科數(shù)學(xué)試卷.files/image578.gif) ,則
,則 考第一次考試文科數(shù)學(xué)試卷.files/image580.gif) ,
,考第一次考試文科數(shù)學(xué)試卷.files/image582.gif) ……8分
……8分
設(shè)考第一次考試文科數(shù)學(xué)試卷.files/image584.gif) ,
,考第一次考試文科數(shù)學(xué)試卷.files/image586.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image588.gif) ,令
,令考第一次考試文科數(shù)學(xué)試卷.files/image590.gif) 解得
解得考第一次考試文科數(shù)學(xué)試卷.files/image592.gif) 或
或考第一次考試文科數(shù)學(xué)試卷.files/image594.gif)
列表如下:
考第一次考試文科數(shù)學(xué)試卷.files/image596.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image598.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image600.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image602.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image604.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image606.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image608.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image610.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image612.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image614.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image616.gif)
__
0
+
考第一次考試文科數(shù)學(xué)試卷.files/image618.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image620.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image621.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image622.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image622.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image624.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image625.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image625.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image620.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image628.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image539.gif) 函數(shù)
函數(shù)考第一次考試文科數(shù)學(xué)試卷.files/image618.gif) 在
在考第一次考試文科數(shù)學(xué)試卷.files/image600.gif) 和
和考第一次考試文科數(shù)學(xué)試卷.files/image608.gif) 上是增函數(shù),在
上是增函數(shù),在考第一次考試文科數(shù)學(xué)試卷.files/image604.gif) 上是減函數(shù)。
上是減函數(shù)。
當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image592.gif) 時(shí),
時(shí),考第一次考試文科數(shù)學(xué)試卷.files/image618.gif) 有極大值
有極大值考第一次考試文科數(shù)學(xué)試卷.files/image637.gif) ;當(dāng)
;當(dāng)考第一次考試文科數(shù)學(xué)試卷.files/image594.gif) 時(shí),
時(shí),考第一次考試文科數(shù)學(xué)試卷.files/image618.gif) 有極小值
有極小值考第一次考試文科數(shù)學(xué)試卷.files/image641.gif) ……10分
……10分
考第一次考試文科數(shù)學(xué)試卷.files/image535.gif) 函數(shù)
函數(shù)考第一次考試文科數(shù)學(xué)試卷.files/image180.gif) 與
與考第一次考試文科數(shù)學(xué)試卷.files/image241.gif) 的圖象有兩個(gè)公共點(diǎn),
的圖象有兩個(gè)公共點(diǎn),考第一次考試文科數(shù)學(xué)試卷.files/image539.gif) 函數(shù)
函數(shù)考第一次考試文科數(shù)學(xué)試卷.files/image618.gif) 與
與考第一次考試文科數(shù)學(xué)試卷.files/image648.gif) 的圖象有兩個(gè)公共點(diǎn)
的圖象有兩個(gè)公共點(diǎn)
考第一次考試文科數(shù)學(xué)試卷.files/image650.gif) 或
或 考第一次考試文科數(shù)學(xué)試卷.files/image652.gif)
考第一次考試文科數(shù)學(xué)試卷.files/image654.gif) ……13分
……13分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com