
題目列表(包括答案和解析)
| x |
| x+1 |
| an+1 |
| an |
| ||
| 2 |
| 1 |
| an |
| 2 |
(1)一個正整數(shù)不是合數(shù)就是質(zhì)數(shù);
(2)x+y是有理數(shù),則x,y都是有理數(shù);
(3)三角形中大角所對的邊大于小角所對的邊;
(4)求證:若x∈R,則方程x2+x+1=0無實根;
(5)x2-4x-7>0.
(Ⅰ)已知函數(shù)![]() .數(shù)列
.數(shù)列![]() 滿足:
滿足:![]() ,且
,且![]() ,記數(shù)列
,記數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .求數(shù)列
.求數(shù)列![]() 的通項公式;并判斷
的通項公式;并判斷![]() 是否仍為數(shù)列
是否仍為數(shù)列![]() 中的項?若是,請證明;否則,說明理由.
中的項?若是,請證明;否則,說明理由.
(Ⅱ)設![]() 為首項是
為首項是![]() ,公差
,公差![]() 的等差數(shù)列,求證:“數(shù)列
的等差數(shù)列,求證:“數(shù)列![]() 中任意不同兩項之和仍為數(shù)列
中任意不同兩項之和仍為數(shù)列![]() 中的項”的充要條件是“存在整數(shù)
中的項”的充要條件是“存在整數(shù)![]() ,使
,使![]() ”.
”.
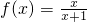 .數(shù)列{an}滿足:an>0,a1=1,且
.數(shù)列{an}滿足:an>0,a1=1,且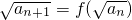 ,記數(shù)列{bn}的前n項和為Sn,且
,記數(shù)列{bn}的前n項和為Sn,且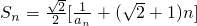 .求數(shù)列{bn}的通項公式;并判斷b4+b6是否仍為數(shù)列{bn}中的項?若是,請證明;否則,說明理由.
.求數(shù)列{bn}的通項公式;并判斷b4+b6是否仍為數(shù)列{bn}中的項?若是,請證明;否則,說明理由.| x |
| x+1 |
| an+1 |
| an |
| ||
| 2 |
| 1 |
| an |
| 2 |
一、選擇題(本大題共12小題,每小題4分,共48分)
1.B 2.A 3.D 4.C 5.D 6.C
7.A 8.C 9.B 10.C 11.A 12.B
二、填空題(本大題共4小題,每小題4分,共16分)
13. 模塊1-2測試題.files/image175.gif)
14. 模塊1-2測試題.files/image176.gif)
15. 增函數(shù)的定義
16. 與該平面平行的兩個平面
三、解答題(本大題共3小題,每小題12分,共36分)
17.(本小題滿分12分)
模塊1-2測試題.files/image178.gif) 解:(Ⅰ)涉及兩個變量,年齡與脂肪含量.
解:(Ⅰ)涉及兩個變量,年齡與脂肪含量.
因此選取年齡為自變量模塊1-2測試題.files/image122.gif) ,脂肪含量為因變量
,脂肪含量為因變量模塊1-2測試題.files/image027.gif) .
.
作散點圖,從圖中可看出模塊1-2測試題.files/image122.gif) 與
與模塊1-2測試題.files/image027.gif) 具有相關(guān)關(guān)系.
具有相關(guān)關(guān)系.
┄┄┄┄┄┄┄┄┄┄┄┄6分
(Ⅱ)模塊1-2測試題.files/image027.gif) 對
對模塊1-2測試題.files/image122.gif) 的回歸直線方程為
的回歸直線方程為
模塊1-2測試題.files/image182.gif) .
.
當模塊1-2測試題.files/image184.gif) 時,
時,模塊1-2測試題.files/image186.gif) ,
,模塊1-2測試題.files/image188.gif) .
.
當模塊1-2測試題.files/image190.gif) 時,
時,模塊1-2測試題.files/image192.gif) ,
,模塊1-2測試題.files/image194.gif) .
.
所以模塊1-2測試題.files/image127.gif) 歲和
歲和模塊1-2測試題.files/image129.gif) 歲的殘差分別為
歲的殘差分別為模塊1-2測試題.files/image196.gif) 和
和模塊1-2測試題.files/image198.gif) .
.
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
證明:由于模塊1-2測試題.files/image200.gif) ,
,模塊1-2測試題.files/image202.gif) ,
,
所以只需證明模塊1-2測試題.files/image204.gif) .
.
展開得模塊1-2測試題.files/image206.gif) ,即
,即模塊1-2測試題.files/image208.gif) .
.
所以只需證模塊1-2測試題.files/image210.gif) .
.
因為模塊1-2測試題.files/image210.gif) 顯然成立,
顯然成立,
所以模塊1-2測試題.files/image133.gif) .┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
18B. (本小題滿分12分)
證明:(Ⅰ)因為模塊1-2測試題.files/image142.gif) ,所以
,所以模塊1-2測試題.files/image212.gif) .
.
由于函數(shù)模塊1-2測試題.files/image135.gif) 是
是模塊1-2測試題.files/image137.gif) 上的增函數(shù),
上的增函數(shù),
所以模塊1-2測試題.files/image214.gif) .
.
同理, 模塊1-2測試題.files/image216.gif) .
.
兩式相加,得模塊1-2測試題.files/image144.gif) .┄┄┄┄┄┄┄┄┄┄┄┄6分
.┄┄┄┄┄┄┄┄┄┄┄┄6分
(Ⅱ)逆命題:
若模塊1-2測試題.files/image144.gif) ,則
,則模塊1-2測試題.files/image142.gif) .
.
用反證法證明
假設模塊1-2測試題.files/image219.gif) ,那么
,那么
模塊1-2測試題.files/image221.gif)
所以模塊1-2測試題.files/image223.gif) .
.
這與模塊1-2測試題.files/image144.gif) 矛盾.故只有
矛盾.故只有模塊1-2測試題.files/image142.gif) ,逆命題得證.
,逆命題得證.
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
解:(Ⅰ)由于模塊1-2測試題.files/image225.gif) ,且
,且模塊1-2測試題.files/image087.gif) .
.
所以當模塊1-2測試題.files/image155.gif) 時,得
時,得模塊1-2測試題.files/image229.gif) ,故
,故模塊1-2測試題.files/image231.gif) .
.
從而模塊1-2測試題.files/image233.gif) .┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分
.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分
(Ⅱ)數(shù)列模塊1-2測試題.files/image146.gif) 不可能為等差數(shù)列,證明如下:
不可能為等差數(shù)列,證明如下:
由模塊1-2測試題.files/image087.gif) ,
,模塊1-2測試題.files/image149.gif) 得
得
若存在模塊1-2測試題.files/image153.gif) ,使
,使模塊1-2測試題.files/image146.gif) 為等差數(shù)列,則
為等差數(shù)列,則模塊1-2測試題.files/image246.gif) ,
,
即模塊1-2測試題.files/image248.gif) ,解得
,解得模塊1-2測試題.files/image231.gif) .
.
于是模塊1-2測試題.files/image251.gif) ,
,模塊1-2測試題.files/image253.gif) .
.
這與模塊1-2測試題.files/image146.gif) 為等差數(shù)列矛盾.所以,對任意
為等差數(shù)列矛盾.所以,對任意模塊1-2測試題.files/image153.gif) ,數(shù)列
,數(shù)列模塊1-2測試題.files/image146.gif) 都不可能是等差數(shù)列.
都不可能是等差數(shù)列.
┄┄┄┄┄┄┄┄┄┄┄┄12分
19B. (本小題滿分12分)
解:(Ⅰ)模塊1-2測試題.files/image258.gif) ,
,模塊1-2測試題.files/image260.gif) .
.
模塊1-2測試題.files/image262.gif) ,
,模塊1-2測試題.files/image264.gif) .┄┄┄┄┄┄┄┄┄┄┄6分
.┄┄┄┄┄┄┄┄┄┄┄6分
(Ⅱ)由(Ⅰ)可得模塊1-2測試題.files/image266.gif) ,
,
模塊1-2測試題.files/image268.gif) ,
,
模塊1-2測試題.files/image270.gif) .
.
猜想:模塊1-2測試題.files/image173.gif) 是公比為
是公比為模塊1-2測試題.files/image272.gif) 的等比數(shù)列.
的等比數(shù)列.
證明如下:因為模塊1-2測試題.files/image274.gif)
模塊1-2測試題.files/image276.gif) ,
,
又模塊1-2測試題.files/image278.gif) ,所以
,所以模塊1-2測試題.files/image280.gif) ,
,
所以數(shù)列模塊1-2測試題.files/image173.gif) 是首項為
是首項為模塊1-2測試題.files/image282.gif) ,公比為
,公比為模塊1-2測試題.files/image272.gif) 的等比數(shù)列.┄┄┄┄┄┄┄┄┄┄┄┄12分
的等比數(shù)列.┄┄┄┄┄┄┄┄┄┄┄┄12分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com