
題目列表(包括答案和解析)
已知函數 其中
其中 為自然對數的底數,
為自然對數的底數,
 .(Ⅰ)設
.(Ⅰ)設 ,求函數
,求函數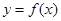 的最值;(Ⅱ)若對于任意的
的最值;(Ⅱ)若對于任意的 ,都有
,都有 成立,求
成立,求 的取值范圍.
的取值范圍.
【解析】第一問中,當 時,
時, ,
, .結合表格和導數的知識判定單調性和極值,進而得到最值。
.結合表格和導數的知識判定單調性和極值,進而得到最值。
第二問中,∵ ,
, ,
,
∴原不等式等價于: ,
,
即 , 亦即
, 亦即
分離參數的思想求解參數的范圍
解:(Ⅰ)當 時,
時, ,
, .
.
當 在
在 上變化時,
上變化時, ,
, 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
|
|
|
- |
|
+ |
|
|
|
|
|
|
|
1/e |
∴ 時,
時, ,
, .
.
(Ⅱ)∵ ,
, ,
,
∴原不等式等價于: ,
,
即 , 亦即
, 亦即 .
.
∴對于任意的 ,原不等式恒成立,等價于
,原不等式恒成立,等價于 對
對 恒成立,
恒成立,
∵對于任意的 時,
時, 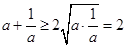 (當且僅當
(當且僅當 時取等號).
時取等號).
∴只需 ,即
,即 ,解之得
,解之得 或
或 .
.
因此, 的取值范圍是
的取值范圍是
給定兩個命題,
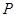 :對任意實數
:對任意實數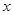 都有
都有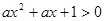 恒成立;
恒成立;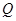 :關于
:關于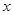 的方程
的方程 有實數根;如果“
有實數根;如果“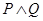 ”為假,且“
”為假,且“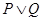 ”為真,求實數
”為真,求實數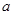 的取值范圍。
的取值范圍。
給定兩個命題, :對任意實數
:對任意實數 都有
都有 恒成立;
恒成立; :關于
:關于 的方程
的方程 有實數根;如果“
有實數根;如果“ ”為假,且“
”為假,且“ ”為真,求實數
”為真,求實數 的取值范圍。
的取值范圍。
 :對任意實數
:對任意實數 都有
都有 恒成立;
恒成立; :關于
:關于 的方程
的方程 有實數根;如果“
有實數根;如果“ ”為假,且“
”為假,且“ ”為真,求實數
”為真,求實數 的取值范圍。
的取值范圍。已知函數![]()
![]() ,函數
,函數![]() 的圖象與
的圖象與![]() 的圖象關于點
的圖象關于點![]() 中心對稱。
中心對稱。
(1)求函數![]() 的解析式;
的解析式;
(2)如果![]() ,
,![]() ,試求出使
,試求出使![]() 成立的
成立的![]() 取值范圍;
取值范圍;
(3)是否存在區間![]() ,使
,使![]() 對于區間內的任意實數
對于區間內的任意實數![]() ,只要
,只要![]() ,且
,且![]() 時,都有
時,都有![]() 恒成立?
恒成立?
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com