
題目列表(包括答案和解析)
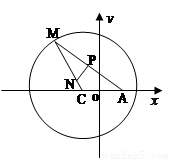
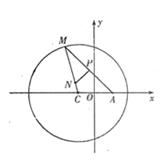 如圖所示,已知圓
如圖所示,已知圓![]() 為圓上一動點,點P在AM上,點N在CM上,且滿足
為圓上一動點,點P在AM上,點N在CM上,且滿足![]() 的軌跡為曲線E.
的軌跡為曲線E.![]()
(I)求曲線E的方程;
(II)過點A且傾斜角是45°的直線l交曲線E于兩點H、Q,求|HQ|.
如圖所示,已知圓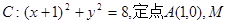 為圓上一動點,點
為圓上一動點,點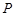 是線段
是線段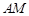 的垂直平分線與直線
的垂直平分線與直線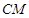 的交點.
的交點.

(1)求點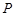 的軌跡曲線
的軌跡曲線 的方程;
的方程;
(2)設(shè)點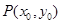 是曲線
是曲線 上任意一點,寫出曲線
上任意一點,寫出曲線 在點
在點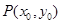 處的切線
處的切線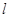 的方程;(不要求證明)
的方程;(不要求證明)
(3)直線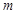 過切點
過切點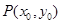 與直線
與直線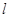 垂直,點
垂直,點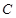 關(guān)于直線
關(guān)于直線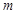 的對稱點為
的對稱點為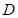 ,證明:直線
,證明:直線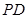 恒過一定點,并求定點的坐標.
恒過一定點,并求定點的坐標.
如圖所示,已知圓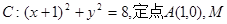 為圓上一動點,點
為圓上一動點,點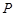 是線段
是線段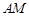 的垂直平分線與直線
的垂直平分線與直線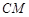 的交點.
的交點.
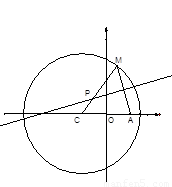
(1)求點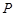 的軌跡曲線
的軌跡曲線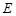 的方程;
的方程;
(2)設(shè)點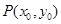 是曲線
是曲線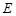 上任意一點,寫出曲線
上任意一點,寫出曲線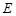 在點
在點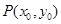 處的切線
處的切線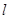 的方程;(不要求證明)
的方程;(不要求證明)
(3)直線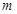 過切點
過切點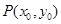 與直線
與直線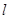 垂直,點
垂直,點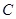 關(guān)于直線
關(guān)于直線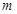 的對稱點為
的對稱點為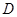 ,證明:直線
,證明:直線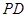 恒過一定點,并求定點的坐標.
恒過一定點,并求定點的坐標.
(12分)如圖所示,已知圓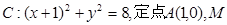 為圓上一動點,點
為圓上一動點,點 在
在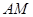 上,點
上,點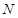 在
在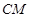 上,且滿足
上,且滿足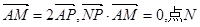 的軌跡為曲線
的軌跡為曲線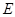 .
.
(1)求曲線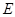 的方程;
的方程;
(2)若直線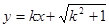 與(1)中所求點
與(1)中所求點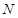 的軌跡
的軌跡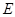 交于不同兩點
交于不同兩點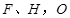 是坐標原點,且
是坐標原點,且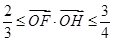 ,求△
,求△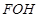 的面積的取值范圍.
的面積的取值范圍.
如圖所示,已知圓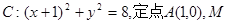 為圓上一動點,點
為圓上一動點,點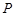 是線段
是線段 的垂直平分線與直線
的垂直平分線與直線 的交點.
的交點.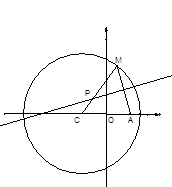
(1)求點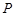 的軌跡曲線
的軌跡曲線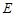 的方程;
的方程;
(2)設(shè)點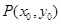 是曲線
是曲線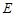 上任意一點,寫出曲線
上任意一點,寫出曲線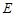 在點
在點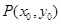 處的切線
處的切線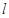 的方程;(不要求證明)
的方程;(不要求證明)
(3)直線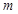 過切點
過切點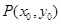 與直線
與直線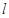 垂直,點
垂直,點 關(guān)于直線
關(guān)于直線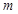 的對稱點為
的對稱點為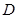 ,證明:直線
,證明:直線 恒過一定點,并求定點的坐標.
恒過一定點,并求定點的坐標.
1、A 2、B 3、B 4、D 5、C 6、C
-解析幾何.files/image114.gif) 7、
7、-解析幾何.files/image116.gif) 8、
8、-解析幾何.files/image118.gif) 9、0
10、
9、0
10、
11、【解】(1)-解析幾何.files/image120.gif)
∴NP為AM的垂直平分線,∴|NA|=|NM|.…………………………2分
又-解析幾何.files/image122.gif)
∴動點N的軌跡是以點C(-1,0),A(1,0)為焦點的橢圓.
且橢圓長軸長為-解析幾何.files/image124.gif) 焦距
焦距-解析幾何.files/image126.gif) ……………5分
……………5分
∴曲線E的方程為-解析幾何.files/image128.gif) ………………6分
………………6分
(2)當直線GH斜率存在時,
設(shè)直線GH方程為-解析幾何.files/image130.gif)
得-解析幾何.files/image132.gif)
設(shè)-解析幾何.files/image134.gif) ……………………8分
……………………8分
-解析幾何.files/image136.gif)
-解析幾何.files/image138.gif) ,
,
-解析幾何.files/image140.gif) ……………………10分
……………………10分
-解析幾何.files/image142.gif)
-解析幾何.files/image144.gif)
又當直線GH斜率不存在,方程為-解析幾何.files/image146.gif)
-解析幾何.files/image148.gif) ……………………………………12分
……………………………………12分
12、【解】(1)由題設(shè)知-解析幾何.files/image150.gif)
由于-解析幾何.files/image104.gif) ,則有
,則有-解析幾何.files/image153.gif) ,所以點A的坐標為
,所以點A的坐標為-解析幾何.files/image155.gif) ,
,
故-解析幾何.files/image157.gif) 所在直線方程為
所在直線方程為-解析幾何.files/image159.gif) ,
………………………………3分
,
………………………………3分
所以坐標原點O到直線-解析幾何.files/image157.gif) 的距離為
的距離為-解析幾何.files/image161.gif) ,
,
又-解析幾何.files/image163.gif) ,所以
,所以-解析幾何.files/image165.gif) ,解得
,解得-解析幾何.files/image167.gif) ,
,
所求橢圓的方程為-解析幾何.files/image169.gif) .……………………………………………5分
.……………………………………………5分
(2)由題意知直線l的斜率存在,設(shè)直線l的方程為-解析幾何.files/image171.gif) ,則有
,則有-解析幾何.files/image173.gif) ,
,
設(shè)-解析幾何.files/image175.gif) ,由于
,由于-解析幾何.files/image112.gif) ,
,
∴-解析幾何.files/image178.gif) ,解得
,解得-解析幾何.files/image180.gif) …………………8分
…………………8分
又Q在橢圓C上,得-解析幾何.files/image182.gif) ,
,
解得-解析幾何.files/image184.gif) ,
…………………………………………………………………………10分
,
…………………………………………………………………………10分
故直線l的方程為-解析幾何.files/image186.gif) 或
或-解析幾何.files/image188.gif) ,
,
即-解析幾何.files/image190.gif) 或
或-解析幾何.files/image192.gif) . ……………………………………………12分
. ……………………………………………12分
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com