
題目列表(包括答案和解析)
已知函數(shù) 的圖象過坐標(biāo)原點(diǎn)O,且在點(diǎn)
的圖象過坐標(biāo)原點(diǎn)O,且在點(diǎn) 處的切線的斜率是
處的切線的斜率是 .
.
(Ⅰ)求實(shí)數(shù) 的值;
的值;
(Ⅱ)求 在區(qū)間
在區(qū)間 上的最大值;
上的最大值;
(Ⅲ)對任意給定的正實(shí)數(shù) ,曲線
,曲線 上是否存在兩點(diǎn)P、Q,使得
上是否存在兩點(diǎn)P、Q,使得 是以O(shè)為直角頂點(diǎn)的直角三角形,且此三角形斜邊中點(diǎn)在
是以O(shè)為直角頂點(diǎn)的直角三角形,且此三角形斜邊中點(diǎn)在 軸上?說明理由.
軸上?說明理由.
【解析】第一問當(dāng) 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
第二問當(dāng) 時,
時, ,令
,令 得
得 ,結(jié)合導(dǎo)數(shù)和函數(shù)之間的關(guān)系得到單調(diào)性的判定,得到極值和最值
,結(jié)合導(dǎo)數(shù)和函數(shù)之間的關(guān)系得到單調(diào)性的判定,得到極值和最值
第三問假設(shè)曲線 上存在兩點(diǎn)P、Q滿足題設(shè)要求,則點(diǎn)P、Q只能在
上存在兩點(diǎn)P、Q滿足題設(shè)要求,則點(diǎn)P、Q只能在 軸兩側(cè)。
軸兩側(cè)。
不妨設(shè) ,則
,則 ,顯然
,顯然
∵ 是以O(shè)為直角頂點(diǎn)的直角三角形,∴
是以O(shè)為直角頂點(diǎn)的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設(shè)要求的兩點(diǎn)P、Q;
(*)若方程(*)有解,存在滿足題設(shè)要求的兩點(diǎn)P、Q;
若方程(*)無解,不存在滿足題設(shè)要求的兩點(diǎn)P、Q.
(Ⅰ)當(dāng) 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①當(dāng) 時,
時, ,令
,令 得
得
當(dāng) 變化時,
變化時, 的變化情況如下表:
的變化情況如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
極小值 |
單調(diào)遞增 |
極大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值為2.
上的最大值為2.
②當(dāng) 時,
時,  .當(dāng)
.當(dāng) 時,
時,  ,
, 最大值為0;
最大值為0;
當(dāng) 時,
時,  在
在 上單調(diào)遞增。∴
上單調(diào)遞增。∴ 在
在 最大值為
最大值為 。
。
綜上,當(dāng) 時,即
時,即 時,
時, 在區(qū)間
在區(qū)間 上的最大值為2;
上的最大值為2;
當(dāng) 時,即
時,即 時,
時, 在區(qū)間
在區(qū)間 上的最大值為
上的最大值為 。
。
(Ⅲ)假設(shè)曲線 上存在兩點(diǎn)P、Q滿足題設(shè)要求,則點(diǎn)P、Q只能在
上存在兩點(diǎn)P、Q滿足題設(shè)要求,則點(diǎn)P、Q只能在 軸兩側(cè)。
軸兩側(cè)。
不妨設(shè) ,則
,則 ,顯然
,顯然
∵ 是以O(shè)為直角頂點(diǎn)的直角三角形,∴
是以O(shè)為直角頂點(diǎn)的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設(shè)要求的兩點(diǎn)P、Q;
(*)若方程(*)有解,存在滿足題設(shè)要求的兩點(diǎn)P、Q;
若方程(*)無解,不存在滿足題設(shè)要求的兩點(diǎn)P、Q.
若 ,則
,則 代入(*)式得:
代入(*)式得:
即 ,而此方程無解,因此
,而此方程無解,因此 。此時
。此時 ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,則
,則
∴ 在
在 上單調(diào)遞增, ∵
上單調(diào)遞增, ∵  ∴
∴ ,∴
,∴ 的取值范圍是
的取值范圍是 。
。
∴對于 ,方程(**)總有解,即方程(*)總有解。
,方程(**)總有解,即方程(*)總有解。
因此,對任意給定的正實(shí)數(shù) ,曲線
,曲線 上存在兩點(diǎn)P、Q,使得
上存在兩點(diǎn)P、Q,使得 是以O(shè)為直角頂點(diǎn)的直角三角形,且此三角形斜邊中點(diǎn)在
是以O(shè)為直角頂點(diǎn)的直角三角形,且此三角形斜邊中點(diǎn)在 軸上
軸上
已知函數(shù)f(x)=ex-ax,其中a>0.
(1)若對一切x∈R,f(x)  1恒成立,求a的取值集合;
1恒成立,求a的取值集合;
(2)在函數(shù)f(x)的圖像上去定點(diǎn)A(x1, f(x1)),B(x2, f(x2))(x1<x2),記直線AB的斜率為k,證明:存在x0∈(x1,x2),使 恒成立.
恒成立.
【解析】解: 令
令 .
.
當(dāng) 時
時 單調(diào)遞減;當(dāng)
單調(diào)遞減;當(dāng) 時
時 單調(diào)遞增,故當(dāng)
單調(diào)遞增,故當(dāng) 時,
時, 取最小值
取最小值
于是對一切 恒成立,當(dāng)且僅當(dāng)
恒成立,當(dāng)且僅當(dāng) . ①
. ①
令 則
則
當(dāng) 時,
時, 單調(diào)遞增;當(dāng)
單調(diào)遞增;當(dāng) 時,
時, 單調(diào)遞減.
單調(diào)遞減.
故當(dāng) 時,
時, 取最大值
取最大值 .因此,當(dāng)且僅當(dāng)
.因此,當(dāng)且僅當(dāng) 時,①式成立.
時,①式成立.
綜上所述, 的取值集合為
的取值集合為 .
.
(Ⅱ)由題意知, 令
令 則
則


令 ,則
,則 .當(dāng)
.當(dāng) 時,
時, 單調(diào)遞減;當(dāng)
單調(diào)遞減;當(dāng) 時,
時, 單調(diào)遞增.故當(dāng)
單調(diào)遞增.故當(dāng) ,
, 即
即
從而 ,
, 又
又

所以
 因?yàn)楹瘮?shù)
因?yàn)楹瘮?shù) 在區(qū)間
在區(qū)間 上的圖像是連續(xù)不斷的一條曲線,所以存在
上的圖像是連續(xù)不斷的一條曲線,所以存在 使
使 即
即 成立.
成立.
【點(diǎn)評】本題考查利用導(dǎo)函數(shù)研究函數(shù)單調(diào)性、最值、不等式恒成立問題等,考查運(yùn)算能力,考查分類討論思想、函數(shù)與方程思想等數(shù)學(xué)方法.第一問利用導(dǎo)函數(shù)法求出 取最小值
取最小值 對一切x∈R,f(x)
對一切x∈R,f(x)  1恒成立轉(zhuǎn)化為
1恒成立轉(zhuǎn)化為 從而得出求a的取值集合;第二問在假設(shè)存在的情況下進(jìn)行推理,然后把問題歸結(jié)為一個方程是否存在解的問題,通過構(gòu)造函數(shù),研究這個函數(shù)的性質(zhì)進(jìn)行分析判斷.
從而得出求a的取值集合;第二問在假設(shè)存在的情況下進(jìn)行推理,然后把問題歸結(jié)為一個方程是否存在解的問題,通過構(gòu)造函數(shù),研究這個函數(shù)的性質(zhì)進(jìn)行分析判斷.
已知數(shù)列 是各項(xiàng)均不為0的等差數(shù)列,公差為d,
是各項(xiàng)均不為0的等差數(shù)列,公差為d, 為其前n項(xiàng)和,且滿足
為其前n項(xiàng)和,且滿足 ,
, .?dāng)?shù)列
.?dāng)?shù)列 滿足
滿足 ,
, ,
, 為數(shù)列
為數(shù)列 的前n項(xiàng)和.
的前n項(xiàng)和.
(1)求數(shù)列 的通項(xiàng)公式
的通項(xiàng)公式 和數(shù)列
和數(shù)列 的前n項(xiàng)和
的前n項(xiàng)和 ;
;
(2)若對任意的 ,不等式
,不等式 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù) 的取值范圍;
的取值范圍;
(3)是否存在正整數(shù)
 ,使得
,使得 成等比數(shù)列?若存在,求出所有
成等比數(shù)列?若存在,求出所有 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【解析】第一問利用在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 時,
時, 滿足
滿足 ,
,
 ,
,

第二問,①當(dāng)n為偶數(shù)時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等號在n=2時取得.
,等號在n=2時取得.
 此時
此時 需滿足
需滿足 .
.
②當(dāng)n為奇數(shù)時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是隨n的增大而增大, n=1時
是隨n的增大而增大, n=1時 取得最小值-6.
取得最小值-6.
 此時
此時 需滿足
需滿足 .
.
第三問 ,
,
若 成等比數(shù)列,則
成等比數(shù)列,則 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
(1)(法一)在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 時,
時, 滿足
滿足 ,
,
 ,
,
 .
.
(2)①當(dāng)n為偶數(shù)時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等號在n=2時取得.
,等號在n=2時取得.
 此時
此時 需滿足
需滿足 .
.
②當(dāng)n為奇數(shù)時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是隨n的增大而增大, n=1時
是隨n的增大而增大, n=1時 取得最小值-6.
取得最小值-6.
 此時
此時 需滿足
需滿足 .
.
綜合①、②可得 的取值范圍是
的取值范圍是 .
.
(3) ,
,
若 成等比數(shù)列,則
成等比數(shù)列,則 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
又 ,且m>1,所以m=2,此時n=12.
,且m>1,所以m=2,此時n=12.
因此,當(dāng)且僅當(dāng)m=2,
n=12時,數(shù)列 中的
中的 成等比數(shù)列
成等比數(shù)列
設(shè)A是由m×n個實(shí)數(shù)組成的m行n列的數(shù)表,滿足:每個數(shù)的絕對值不大于1,且所有數(shù)的和為零,記s(m,n)為所有這樣的數(shù)表構(gòu)成的集合。
對于A∈S(m,n),記ri(A)為A的第ⅰ行各數(shù)之和(1≤ⅰ≤m),Cj(A)為A的第j列各數(shù)之和(1≤j≤n):
記K(A)為∣r1(A)∣,∣R2(A)∣,…,∣Rm(A)∣,∣C1(A)∣,∣C2(A)∣,…,∣Cn(A)∣中的最小值。
(1) 對如下數(shù)表A,求K(A)的值;
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)設(shè)數(shù)表A∈S(2,3)形如
|
1 |
1 |
c |
|
a |
b |
-1 |
求K(A)的最大值;
(3)給定正整數(shù)t,對于所有的A∈S(2,2t+1),求K(A)的最大值。
【解析】(1)因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912442510881234/SYS201207091244551401982556_ST.files/image001.png">,
所以
(2) 不妨設(shè) .由題意得
.由題意得 .又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912442510881234/SYS201207091244551401982556_ST.files/image006.png">,所以
.又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912442510881234/SYS201207091244551401982556_ST.files/image006.png">,所以 ,
,
于是 ,
, ,
,

所以 ,當(dāng)
,當(dāng) ,且
,且 時,
時, 取得最大值1。
取得最大值1。
(3)對于給定的正整數(shù)t,任給數(shù)表 如下,
如下,
|
|
|
… |
|
|
|
|
… |
|
任意改變A的行次序或列次序,或把A中的每一個數(shù)換成它的相反數(shù),所得數(shù)表
 ,并且
,并且 ,因此,不妨設(shè)
,因此,不妨設(shè) ,
,
且
 。
。
由 得定義知,
得定義知, ,
,

又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912442510881234/SYS201207091244551401982556_ST.files/image030.png">
所以


所以,
對數(shù)表 :
:
|
1 |
1 |
… |
1 |
|
… |
|
|
|
|
… |
|
-1 |
… |
-1 |
則 且
且 ,
,
綜上,對于所有的 ,
, 的最大值為
的最大值為
已知函數(shù) ,其中
,其中 .
.
(1)若 在
在 處取得極值,求曲線
處取得極值,求曲線 在點(diǎn)
在點(diǎn)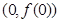 處的切線方程;
處的切線方程;
(2)討論函數(shù) 在
在 的單調(diào)性;
的單調(diào)性;
(3)若函數(shù) 在
在 上的最小值為2,求
上的最小值為2,求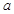 的取值范圍.
的取值范圍.
【解析】第一問, 因
因 在
在 處取得極值
處取得極值
所以, ,解得
,解得 ,此時
,此時 ,可得求曲線
,可得求曲線 在點(diǎn)
在點(diǎn)
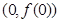 處的切線方程為:
處的切線方程為:
第二問中,易得 的分母大于零,
的分母大于零,
①當(dāng) 時,
時,
 ,函數(shù)
,函數(shù) 在
在 上單調(diào)遞增;
上單調(diào)遞增;
②當(dāng) 時,由
時,由 可得
可得 ,由
,由 解得
解得
第三問,當(dāng) 時由(2)可知,
時由(2)可知, 在
在 上處取得最小值
上處取得最小值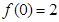 ,
,
當(dāng) 時由(2)可知
時由(2)可知 在
在 處取得最小值
處取得最小值 ,不符合題意.
,不符合題意.
綜上,函數(shù) 在
在 上的最小值為2時,求
上的最小值為2時,求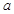 的取值范圍是
的取值范圍是
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com