題目列表(包括答案和解析)
已知偶函數y=f(x)在區間〔-1,0〕是減函數,又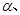
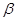是銳角三角形的兩個內角,則（ ）
A f(sin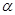
)＞f(cos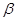) B
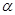f(sin)＜ f(cos)
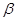C f(sin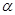)＞f(sin)
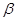D f(cos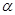)＜f(cos)
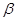A．f(sinα)＞f(cosβ) B．f(sinα)＜f(cosβ)
C．f(sinα)＞f(sinβ) D．f(cosα)＞f(cosβ)
已知偶函數y= f(x)有四個零點，則方程f(x)=0的所有實數根之和為（ ）
A．4 B．2 C．1 D．0
已知偶函數y=f(x)在[－1，0]上為單調遞減函數，又
、
為銳角三角形的兩內角，則
．（填“>”或“=”或“<”）
1――12 A B B B B C D D C A C B
13、1 14、e 15、
16、①②④
17、解
在
上是增函數，
方程
=x2 + (m ? 2 )x + 1 = 0的兩個根在0至3之間
∴
∴
∴
＜m≤0
依題意得：m的取值范圍是:＜m≤-1或m＞0
18、解：（1）
,
當a=1時 解集為
當a>1時，解集為
，
當0<a<1時，解集為
；
（2）依題意知f(1)是f(x)的最小值，又f(1)不可能是端點值，則f(1)是f(x)的一個極小值，由
，
19、解：（1）當
所以f(-x)＝-(-x)2-(-x)+5=-x2+x+5，
所以f(x)=
（2）由題意，不妨設Ａ點在第一象限，坐標為(t,-t2-t+5)其中，
，
則S(t)=S ABCD=2t(-t2-t+5)=-2t3-2t2+10t.
，
令
得
（舍去），t2=1.
當
時
，所以S(t)在
上單調遞增，在
上單調遞減，
所以當t=1時，ABCD的面積取得極大值也是S(t)在上的最大值。
從而當t=1時，矩形ABCD的面積取得最大值6.
20、解：
21、解：
，
令
，要使
在其定義域內為單調函數，只需
在內滿足：
或
恒成立.
① 當
時，
，∵
，∴
，∴
，
∴在內為單調遞減.
② 當
時，，對稱軸為
， ∴
.
只需
，即
時，
，
∴在內為單調遞增。
③當
時，，對稱軸為
.
只需
，即
時在恒成立.
綜上可得，或.
22、解：（Ⅰ）
同理，令
∴f(x)單調遞增區間為
，單調遞減區間為
.
由此可知
（Ⅱ）由（I）可知當
時，有
，
即
.
.
（Ⅲ） 設函數
∴函數
）上單調遞增，在
上單調遞減.
∴的最小值為
，即總有
而
即
令
則
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com