
題目列表(包括答案和解析)
設![]() 是定義在
是定義在![]() 上的函數,用分點
上的函數,用分點
![]()
將區間![]() 任意劃分成個小區間,如果存在一個常數
任意劃分成個小區間,如果存在一個常數![]() ,使得和式
,使得和式![]() (
(![]() )恒成立,則稱
)恒成立,則稱![]() 為
為![]() 上的有界變差函數.
上的有界變差函數.
(1)函數![]() 在
在![]() 上是否為有界變差函數?請說明理由;
上是否為有界變差函數?請說明理由;
(2)設函數![]() 是
是![]() 上的單調遞減函數,證明:
上的單調遞減函數,證明:![]() 為
為![]() 上的有界變差函數;
上的有界變差函數;
(3)若定義在![]() 上的函數
上的函數![]() 滿足:存在常數
滿足:存在常數![]() ,使得對于任意的
,使得對于任意的![]() 、
、![]() 時,
時,![]() .證明:
.證明:![]() 為
為![]() 上的有界變差函數.
上的有界變差函數.
(本小題滿分14分)
設 是定義在
是定義在 上的函數,用分點
上的函數,用分點
將區間 任意劃分成
任意劃分成 個小區間,如果存在一個常數
個小區間,如果存在一個常數 ,使得和式
,使得和式 (
( )恒成立,則稱
)恒成立,則稱 為
為 上的有界變差函數.
上的有界變差函數.
(1)函數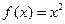 在
在 上是否為有界變差函數?請說明理由;
上是否為有界變差函數?請說明理由;
(2)設函數 是
是 上的單調遞減函數,證明:
上的單調遞減函數,證明: 為
為 上的有界變差函數;
上的有界變差函數;
(3)若定義在 上的函數
上的函數 滿足:存在常數
滿足:存在常數 ,使得對于任意的
,使得對于任意的 、
、 時,
時, .證明:
.證明: 為
為 上的有界變差函數.
上的有界變差函數.
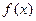 是定義在
是定義在 上的函數,用分點
上的函數,用分點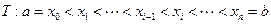
 任意劃分成
任意劃分成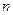 個小區間,如果存在一個常數
個小區間,如果存在一個常數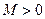 ,使得和式
,使得和式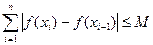 (
(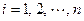 )恒成立,則稱
)恒成立,則稱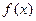 為
為 上的有界變差函數.
上的有界變差函數.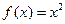 在
在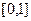 上是否為有界變差函數?請說明理由;
上是否為有界變差函數?請說明理由;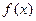 是
是 上的單調遞減函數,證明:
上的單調遞減函數,證明: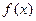 為
為 上的有界變差函數;
上的有界變差函數; 上的函數
上的函數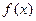 滿足:存在常數
滿足:存在常數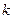 ,使得對于任意的
,使得對于任意的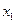 、
、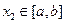 時,
時,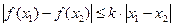 .證明:
.證明: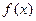 為
為 上的有界變差函數.
上的有界變差函數.| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| f(b)-f(a) |
| b-a |
| 1 |
| 2 |
| 1 |
| 2 |
一、填空題(本大題滿分48分,每小題4分,共12小題)
1..files\image179.gif) ; 2.
; 2..files\image181.gif) ; 3.
; 3..files\image183.gif) ; 4.
; 4..files\image185.gif) ; 5.
; 5..files\image187.gif) ;
;
6..files\image189.gif) ; 7.
; 7..files\image181.gif) ; 8.
; 8..files\image191.gif) ; 9.
; 9..files\image193.gif) ; 10.
; 10..files\image195.gif) ;
;
11..files\image197.gif) ; 12.
; 12..files\image199.gif) .
.
二、選擇題(本大題滿分16分,每小題4分,共4小題)
13.C; 14.A; 15.B; 16.C;
三、解答題(本大題滿分86分,本大題共有6題)
17.(1).files\image201.gif) ;
;
.files\image203.gif)
(2).files\image205.gif) ;
; .files\image207.gif)
18.1號至4號正四棱柱形容器是體積依次為.files\image209.gif) 。
。
∵ .files\image110.gif) ,
,.files\image212.gif) ,
,
∴ 存在必勝方案,即選擇3號和4號容器。
19.(1)∵ 由正弦定理,.files\image214.gif) ,∴
,∴ .files\image216.gif) ,
,.files\image218.gif) 。
。
∵ .files\image220.gif) , ∴
, ∴ .files\image222.gif) ,即
,即.files\image224.gif) 。∴
。∴ .files\image226.gif) 。
。
(2)∵ .files\image228.gif) ,
,
∴ .files\image230.gif) 。
。
20.(1)設放水.files\image125.gif) 分鐘內水箱中的水量為
分鐘內水箱中的水量為.files\image232.gif) 升
升
依題意得.files\image234.gif) ;
;
.files\image236.gif) 分鐘時,水箱的水量
分鐘時,水箱的水量.files\image238.gif) 升, 放水后
升, 放水后.files\image240.gif) 分鐘水箱內水量接近最少;
分鐘水箱內水量接近最少;
(2)該淋浴器一次有.files\image135.gif) 個人連續洗浴, 于是,
個人連續洗浴, 于是,.files\image243.gif) ,
,.files\image245.gif)
.files\image247.gif)
所以,一次可最多連續供7人洗浴。
21.(1)由.files\image249.gif) 及
及.files\image251.gif)
.files\image253.gif) ,∴
,∴.files\image255.gif) 時
時.files\image257.gif) 成等比數列。
成等比數列。
(2)因.files\image259.gif) ,由(1)知,
,由(1)知,.files\image261.gif) ,故
,故.files\image263.gif) 。
。
(3)設存在.files\image265.gif) ,使得
,使得.files\image267.gif) 成等差數列,則
成等差數列,則.files\image269.gif) ,
,
即.files\image271.gif)
.files\image273.gif) 因
因.files\image265.gif) ,所以
,所以.files\image275.gif) ,
,
∴不存在.files\image277.gif) 中的連續三項使得它們可以構成等差數列。
中的連續三項使得它們可以構成等差數列。
22.(1)解:設.files\image279.gif) 為函數
為函數.files\image281.gif) 圖像的一個對稱點,則
圖像的一個對稱點,則.files\image283.gif) 對于
對于.files\image285.gif) 恒成立.即
恒成立.即.files\image287.gif) 對于
對于.files\image285.gif) 恒成立,
恒成立,
.files\image289.gif) 由
由.files\image291.gif) ,故
,故.files\image293.gif) 圖像的一個對稱點為
圖像的一個對稱點為.files\image295.gif) .
.
(2)解:假設.files\image297.gif) 是函數
是函數.files\image299.gif) (
(.files\image301.gif) 的圖像的一個對稱點,
的圖像的一個對稱點,
則.files\image303.gif) (
(.files\image301.gif) 對于
對于.files\image285.gif) 恒成立,
恒成立,
即.files\image306.gif) 對于
對于.files\image285.gif) 恒成立,因為
恒成立,因為.files\image308.gif) ,所以
,所以.files\image306.gif) 不
不
恒成立,
即函數.files\image299.gif) (
(.files\image301.gif) 的圖像無對稱點.
的圖像無對稱點.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com