湖北省武漢市教科院2009屆高三第一次調(diào)考數(shù)學(xué)文科試卷
本試卷共150分。考試用時(shí)120分鐘。
注意事項(xiàng):
1.答卷前,考生務(wù)必將自己的姓名、準(zhǔn)考證號(hào)填寫(xiě)在試題卷的答題卡上,并將準(zhǔn)考證號(hào)條形碼粘貼在答題卡上的指定位置。
2.選擇題選出答案后,用2B鉛筆把答題卡上對(duì)應(yīng)題目的答案標(biāo)號(hào)涂黑,如需改動(dòng),用橡皮擦干凈后,再選涂其他答案標(biāo)號(hào)。非選擇題用黑色墨水的簽字筆或鋼筆直接答在答題卡上。答在試題卷上無(wú)效。
3.考試結(jié)束,監(jiān)考人員將本試題和答題卡一并收回。
4.注明文科做的理科不做,注明理科做的文科不做。
參考公式:
如果事件A、B互斥,那么
P(A+B)=P(A)+P(B)
如果事件A、B相互獨(dú)立,那么
P(A?B)=P(A)?P(B)
如果事件A在一次試驗(yàn)中發(fā)生的概率是P,那么n次獨(dú)立重復(fù)試驗(yàn)中恰好發(fā)生k次的概率

球的表面積公式

其中R表示球的半徑
球的體積公式

其中R表示球的半徑
一、選擇題:本大題共10小題,每小題5分,共50分,在每小題給出的四個(gè)選項(xiàng)中,只有一次是符合題目要求的。
1.已知集合 = ( )
= ( )
試題詳情
試題詳情
2.“p或q是假命題”是“非p為真命題”的 ( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分又不必要條件
試題詳情
3.雙曲線 的兩近漸近線和直線x=2圍成一個(gè)三角形區(qū)域(含邊界),則該區(qū)域可表示為 ( )
的兩近漸近線和直線x=2圍成一個(gè)三角形區(qū)域(含邊界),則該區(qū)域可表示為 ( )
試題詳情
試題詳情
4.(文科)在等比數(shù)列 中,若
中,若 = ( )
= ( )
A.100 B.80 C.95 D.135
試題詳情
(理科)已知Sn表示等差數(shù)列 的前n項(xiàng)和,且
的前n項(xiàng)和,且 = ( )
= ( )
試題詳情
試題詳情
5.(文科)已知函數(shù) ,則下列命題正確的是 ( )
,則下列命題正確的是 ( )
試題詳情
A. 是周期為1的奇函數(shù) B.
是周期為1的奇函數(shù) B. 是周期為2的偶函數(shù)
是周期為2的偶函數(shù)
試題詳情
C. 是周期為1的非奇非偶數(shù) D.
是周期為1的非奇非偶數(shù) D. 是周期為2的非奇非偶函數(shù)
是周期為2的非奇非偶函數(shù)
試題詳情
(理科)△ABC中, 的面積為 ( )
的面積為 ( )
試題詳情
試題詳情
6.已知直線 、
、 ,下列命題中的真命題是 ( )
,下列命題中的真命題是 ( )
試題詳情
A.如果 、
、 ;
;
試題詳情
B.如果 、
、 ;
;
試題詳情
C. 、
、 ;
;
試題詳情
D. 、
、 ;
;
試題詳情
7.已知 等于 ( )
等于 ( )
試題詳情
試題詳情
8.設(shè) 上的兩個(gè)函數(shù),若對(duì)任意的
上的兩個(gè)函數(shù),若對(duì)任意的 ,都有
,都有
試題詳情
 上是“密切函數(shù)”,[a,b]稱(chēng)為“密切區(qū)間”,設(shè)
上是“密切函數(shù)”,[a,b]稱(chēng)為“密切區(qū)間”,設(shè) 上是“密切函數(shù)”,則它的“密切區(qū)間”可以是 ( )
上是“密切函數(shù)”,則它的“密切區(qū)間”可以是 ( )
A.[1,4] B.[2,3] C.[3,4] D.[2,4]
試題詳情
試題詳情
A.最大值 B.最大值1 C.最小值
B.最大值1 C.最小值 D.最小值1
D.最小值1
試題詳情
|
試題詳情
A.(0,3) B.( ) C.(0,4) D.(0, ) C.(0,4) D.(0, ) ) 試題詳情
10.一個(gè)質(zhì)量均勻的正四面體型的骰子,其四個(gè)面上分別標(biāo)有數(shù)字1,2,3,4,若連續(xù)投擲三次,取三次面向下的數(shù)字分別作為三角形的邊長(zhǎng),則其能構(gòu)成鈍角三角形的概率為 ( ) 試題詳情
試題詳情
二、填空題:本大題共5小題,每小題5分,共25分,把答案填在題中的橫線上。 11.設(shè)二項(xiàng)式 的展開(kāi)式的各項(xiàng)系數(shù)的和為p,所有二項(xiàng)式系數(shù)的和為q,且p+q=272,則n的值為
。 的展開(kāi)式的各項(xiàng)系數(shù)的和為p,所有二項(xiàng)式系數(shù)的和為q,且p+q=272,則n的值為
。 試題詳情
12.在航天員進(jìn)行的一項(xiàng)太空試驗(yàn)中,先后要實(shí)施6個(gè)程序,其中程序A只能出現(xiàn)在第一步或最后一步,程序B和C實(shí)施時(shí)必須相鄰,則實(shí)施程序的編排方法共有 種。 試題詳情
13.已知圓 軸交于A、B兩點(diǎn),圓心為P,若 軸交于A、B兩點(diǎn),圓心為P,若 ,則c的值等于
。 ,則c的值等于
。 試題詳情
14.(文科)已知 方向上的投影為 。 方向上的投影為 。 試題詳情
(理科)平面上的向量 若向量 若向量 試題詳情
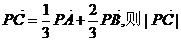 的最大值為 。 的最大值為 。 試題詳情
15.(文科)不等式 的解集為
。 的解集為
。 試題詳情
(理科)對(duì)于 的取值范圍是
。 的取值范圍是
。 試題詳情
三、解答題:本大題共6小題,共75分,解答應(yīng)寫(xiě)出文字說(shuō)明,推理過(guò)程或演算步驟。
試題詳情
已知向量 試題詳情
(1)(文科)若 的單調(diào)遞減區(qū)間; 的單調(diào)遞減區(qū)間; 試題詳情
(2)(理科)若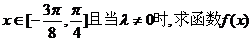 的單調(diào)遞減區(qū)間; 的單調(diào)遞減區(qū)間; 試題詳情
(3)當(dāng) 的圖象的變換過(guò)程。 的圖象的變換過(guò)程。 試題詳情
試題詳情
如圖,在直三棱柱ABC―A1B1C1中, ,直線B1C與 ,直線B1C與 平面ABC成30°角。
(1)求證:平面B1AC⊥平面ABB1A1;
(2)(文科)求二面角B―B1C―A的正切值;
(3)(理科)求直線A1C與平面B1AC所成的角的正弦值。 試題詳情
|
|
|
試題詳情
18.(本小題滿(mǎn)分12分)
(文科)有A、B、C、D、E共5個(gè)口袋,每個(gè)口袋裝有大小和質(zhì)量均相同的4個(gè)紅球和2個(gè)黑球,現(xiàn)每次從其中一個(gè)口袋中摸出3個(gè)球,規(guī)定:若摸出的3個(gè)球恰為2個(gè)紅球和1個(gè)黑球,則稱(chēng)為最佳摸球組合。
(1)求從口袋A中摸出的3個(gè)球?yàn)樽罴衙蚪M合的概率;
(2)現(xiàn)從每個(gè)口袋中摸出3個(gè)球,求恰有3個(gè)口袋中摸出的球是最佳摸球組合的概率。 試題詳情
(理科)在某校運(yùn)動(dòng)會(huì)中,甲、乙、丙三支足球隊(duì)進(jìn)行單循環(huán)賽(即每?jī)申?duì)比賽一場(chǎng))共賽三場(chǎng),每場(chǎng)比賽勝者得3分,負(fù)者得0分,沒(méi)有平局。在每一場(chǎng)比賽中,甲勝乙的概率為 ,甲勝丙的概率為 ,甲勝丙的概率為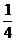 ,乙勝丙的概率為 ,乙勝丙的概率為 ; ;
(1)求甲隊(duì)獲第一名且丙隊(duì)獲第二名的概率; 試題詳情
(2)設(shè)在該次比賽中,甲隊(duì)得分為 的分布列和數(shù)學(xué)期望。 的分布列和數(shù)學(xué)期望。 試題詳情
試題詳情
(文科)已知函數(shù) 試題詳情
(1)求 的值; 的值; 試題詳情
(2)當(dāng) 是否存在最小值?若存在,求出 是否存在最小值?若存在,求出 的最小值;若不存在,請(qǐng)說(shuō)明理由。 的最小值;若不存在,請(qǐng)說(shuō)明理由。 試題詳情
(理科)定義在R上的函數(shù)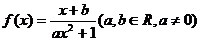 是奇函數(shù),當(dāng)且僅當(dāng) 是奇函數(shù),當(dāng)且僅當(dāng) 取得最大值。 取得最大值。
(1)求a、b的值; 試題詳情
(2)若方程 上有且僅有兩個(gè)不同實(shí)根,求實(shí)數(shù)m的取值 上有且僅有兩個(gè)不同實(shí)根,求實(shí)數(shù)m的取值 范圍。 試題詳情
試題詳情
(1)求數(shù)列 的通項(xiàng)公式; 的通項(xiàng)公式; 試題詳情
(2)設(shè) ,求數(shù)列 ,求數(shù)列 的前n項(xiàng)和Tn; 的前n項(xiàng)和Tn; 試題詳情
(3)(理科)設(shè)各項(xiàng)均不為0的數(shù)列 中,所有滿(mǎn)足 中,所有滿(mǎn)足 的正整數(shù)m的個(gè)數(shù),稱(chēng)為這個(gè)數(shù)列 的正整數(shù)m的個(gè)數(shù),稱(chēng)為這個(gè)數(shù)列 的變號(hào)數(shù),若 的變號(hào)數(shù),若 ,求數(shù)列 ,求數(shù)列 的變號(hào)數(shù)。 的變號(hào)數(shù)。 試題詳情
21.(本小題滿(mǎn)分13分)如圖,設(shè)F是橢圓 的左焦點(diǎn),直線l為其左準(zhǔn)線,直線l與x軸交于點(diǎn)P,線段MN為橢圓的長(zhǎng)軸,已知 的左焦點(diǎn),直線l為其左準(zhǔn)線,直線l與x軸交于點(diǎn)P,線段MN為橢圓的長(zhǎng)軸,已知 試題詳情
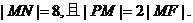
(1)求橢圓C的標(biāo)準(zhǔn)方程;
(2)若過(guò)點(diǎn)P的直線與橢圓相交于不同兩點(diǎn)A、B求證:∠AFM=∠BFN;
(3)(理科)求三角形ABF面積的最大值。 試題詳情
第Ⅰ卷(選擇題,共50分) 1―3 AAD 4(文)D(理)B 5(文)B(理)C
1.3.5 第Ⅱ卷(非選擇題,共100分) 二、填空題 11.4 12.96 13.-3 14.(文) (理) (理) 15.(文) (理) (理) 三、解答題 16.解:(1)      …………(4分) …………(4分)
(1)(文科)在 時(shí), 時(shí),   在 時(shí), 時(shí), 為減函數(shù) 為減函數(shù) 從而 的單調(diào)遞減區(qū)間為 的單調(diào)遞減區(qū)間為 ;…………(文8分) ;…………(文8分)
(2)(理科)  當(dāng) 時(shí),由 時(shí),由 得單調(diào)遞減區(qū)間為 得單調(diào)遞減區(qū)間為 同理,當(dāng) 時(shí),函數(shù)的單調(diào)遞減區(qū)間為 時(shí),函數(shù)的單調(diào)遞減區(qū)間為 …………(理8分) …………(理8分)
(3)當(dāng) ,變換過(guò)程如下: ,變換過(guò)程如下: 1°將 的圖象向右平移 的圖象向右平移 個(gè)單位可得函數(shù) 個(gè)單位可得函數(shù) 的圖象。 的圖象。 2°將所得函數(shù)圖象上每個(gè)點(diǎn)的縱坐標(biāo)擴(kuò)大為原來(lái)的 倍,而橫坐標(biāo)保持不變,可得函數(shù) 倍,而橫坐標(biāo)保持不變,可得函數(shù) 的圖象。 的圖象。 3°再將所得圖象向上平移一個(gè)單位,可得 的圖象……(12分) 的圖象……(12分)
(其它的變換方法正確相應(yīng)給分) 17.解:(1) 三棱柱ABC―A1B1C1為直三棱柱 三棱柱ABC―A1B1C1為直三棱柱  底面ABC 底面ABC 又 AC AC 面ABC 面ABC  AC AC 又  又 AC AC 面B1AC 面B1AC  …………(6分) …………(6分)
(2) 三棱柱ABC―A1B1C1為直三棱柱 三棱柱ABC―A1B1C1為直三棱柱  底面ABC 底面ABC  為直線B1C與平面ABC所成的角,即 為直線B1C與平面ABC所成的角,即 過(guò)點(diǎn)A作AM⊥BC于M,過(guò)M作MN⊥B1C于N,加結(jié)AN。 ∴平面BB1CC1⊥平面ABC ∴AM⊥平面BB1C1C 由三垂線定理知AN⊥B1C從而∠ANM為二面角B―B1C―A的平面角。 設(shè)AB=BB1= 在Rt△B1BC中,BC=BB1

即二面角B―B1C―A的正切值為 …………(文12分) …………(文12分)
(3)(理科)過(guò)點(diǎn)A1作A1H⊥平面B1AC于H,連結(jié)HC,則 ∠A1CH為直線A1C與平面B1AC所成的角 由 知 知  在Rt ………………(理12分) ………………(理12分) 18.解:(文科)(1)從口袋A中摸出的3個(gè)球?yàn)樽罴衙蚪M合即為從口袋A中摸出2個(gè)紅球和1個(gè)黑球,其概率為  ………………………………(6分) ………………………………(6分)
(2)由題意知:每個(gè)口袋中摸球?yàn)樽罴呀M合的概率相同,從5個(gè)口袋中摸球可以看成5次獨(dú)立重復(fù)試難,故所求概率為  ……………………………………(12分) ……………………………………(12分)
(理科)(1)設(shè)用隊(duì)獲第一且丙隊(duì)獲第二為事件A,則  ………………………………………(6分) ………………………………………(6分)
(2) 可能的取值為0,3,6;則 可能的取值為0,3,6;則 甲兩場(chǎng)皆輸: 甲兩場(chǎng)只勝一場(chǎng):
| | | | | |




 = ( )
= ( ) B.
B. C.
C. D.
D.
 的兩近漸近線和直線x=2圍成一個(gè)三角形區(qū)域(含邊界),則該區(qū)域可表示為 ( )
的兩近漸近線和直線x=2圍成一個(gè)三角形區(qū)域(含邊界),則該區(qū)域可表示為 ( )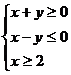 B.
B. C.
C. D.
D.
 中,若
中,若 = ( )
= ( ) 的前n項(xiàng)和,且
的前n項(xiàng)和,且 = ( )
= ( ) B.
B. C.
C. D.
D.
 ,則下列命題正確的是 ( )
,則下列命題正確的是 ( ) 是周期為1的奇函數(shù) B.
是周期為1的奇函數(shù) B. 是周期為2的偶函數(shù)
是周期為2的偶函數(shù) 是周期為1的非奇非偶數(shù) D.
是周期為1的非奇非偶數(shù) D. 是周期為2的非奇非偶函數(shù)
是周期為2的非奇非偶函數(shù) 的面積為 ( )
的面積為 ( ) B.
B. C.
C. D.
D.
 、
、 ,下列命題中的真命題是 ( )
,下列命題中的真命題是 ( ) 、
、 ;
; 、
、 ;
; 、
、 ;
; 、
、 ;
; 等于 ( )
等于 ( ) B.
B. C.
C. D.
D.
 上的兩個(gè)函數(shù),若對(duì)任意的
上的兩個(gè)函數(shù),若對(duì)任意的 ,都有
,都有 上是“密切函數(shù)”,[a,b]稱(chēng)為“密切區(qū)間”,設(shè)
上是“密切函數(shù)”,[a,b]稱(chēng)為“密切區(qū)間”,設(shè) 上是“密切函數(shù)”,則它的“密切區(qū)間”可以是 ( )
上是“密切函數(shù)”,則它的“密切區(qū)間”可以是 ( ) 落在經(jīng)過(guò)點(diǎn)(6,―2)且方向向量為
落在經(jīng)過(guò)點(diǎn)(6,―2)且方向向量為 的直線
的直線 有 ( )
有 ( ) B.最大值
B.最大值 D.最小值1
D.最小值1