
2008-2009學年度日照市五蓮第一學期八年級學科學業水平監測
數學試卷
(時間l00分鐘 滿分l20分)
一、選擇題:(本題共l2小題,第l-8小題,每小題3分,第9-12小題,每小題4分,共40分。在每小題給出的四個選項中,只有一項是正確的)
1.在實數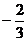 ,0,
,0,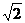 ,
, ,
,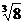 中,無理數有
中,無理數有
A.1個 B.2個 C.3個 D.4個
2.l6的平方根是
A.4 B.士
3.下列運算正確的是
A. B.
B.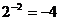
C. D.
D.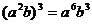
4.任意給定一個非零數,按下列程序計算,最后輸出的結果是

A.m B.m
5.下列各條件中,不能唯一作直角三角形的是
A.已知兩條直角邊 B.已知一銳角及斜邊
C.已知一銳角及其鄰邊 D.已知一銳角及其對邊
6.一個正方體的水晶磚,體積為l
A.
C.
7.如果x2+mx+16是一個完全平方式,那么m的值為
A.8 B.-
8.已知等腰三角形的一個內角為50°,則這個等腰三角形的頂角為
A.50° B.80° C.50°或80° D.40°或65°
9.某蓄水池的橫斷面示意圖如下圖,分深水區和淺水區,如果這個注滿水的蓄水池以固定的流量把水全部放出.下面的圖像能大致表示水的深度h和放水時間t之間的關系的是
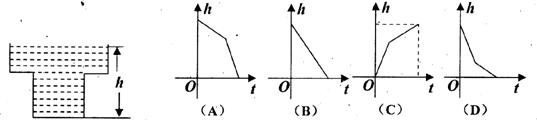
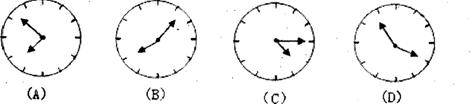
10.小華在鏡中看到身后墻上的鐘,你認為實際時間最接近8點的是
11.如圖,每個小正方形的邊長為l,把陰影部分剪下來,用剪下來的陰影部分拼成一個正方形,那么新正方形的邊長是

A.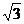 B.
B.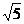 D.
D.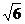
12.甲、乙兩同學騎自行車從A地沿同一條路到B地,已知乙比甲先出發,他們離出發地的距離s(km)和騎行時間t(h)之間的函數關系如圖所示,給出下列說法:
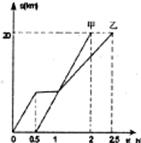
(1)他們都騎行了
(2)乙在途中停留了0.5h;
(3)甲、乙兩人同時到達目的地;
(4)相遇后,甲的速度小于乙的速度.
根據圖像信息,以上說法正確的有
A.1個 B.2個 C.3個 D.4個
二、填空題:(本題共6小題,每小題3分,共18分。請把最終結果直接填在橫線上)
13.因式分解: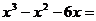 ___________.
___________.
14.如果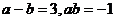 ,則
,則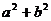 的值等于__________.
的值等于__________.
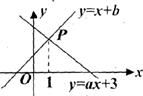
15.如圖,已知函數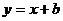 和
和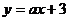 的圖像交點為
的圖像交點為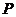 ,則不等式
,則不等式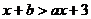 的解集__________.
的解集__________.
16.若直線y=kx+3與坐標軸所圍成的三角形的面積為l2,則k的值為__________.
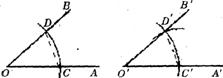
17.用直尺和圓規作一個角等于已知角的示意圖如下圖所示,則說明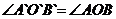 的依據是__________________.
的依據是__________________.
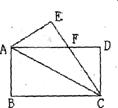
18.如圖將長方形ABCD沿AC折疊,使點B落在點E處,若長方形ABCD的周長為
三、解答題:(本題共6小題,共62分.解答題都應寫出文字說明、證明過程或推演步驟)
19.(每小題6分,共l2分)
(1)已知: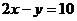 ,求
,求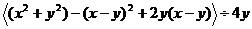 的值.
的值.
(2)分解因式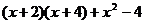 .
.
20.(本題滿分6分)
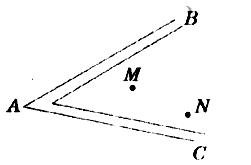
如圖,某中學兩個班的學生分別在M、N兩處參加植樹勞動,現要在道路AB、AC的交叉區域內設置一個茶水供應點P,使點P到點M,N的距離相等,且到兩條道路的距離也相等,現在請你畫出點P的位置的示意圖(不寫作法,只保留作圖痕跡)。
21.(本題滿分l0分)
兩個大小不同的等腰直角三角形三角板如圖1所示放置,圖2是由它抽象出的幾何圖形,B,C,E在同一條直線上,連結DC.
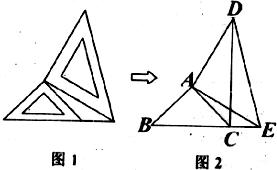
(1)請找出 圖2中的全等三角形,并給予證明(說明:結論中不得含有未標識的字母);
(2)證明:DC⊥BE
22.(本題滿分12分)
已知:點O到△ABC的兩邊AB、AC所在真線的距離相等,且OB=OC。
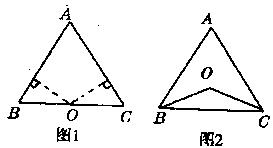
(1)如圖l,若點O在BC上,求證:AB=AC;
(2)如圖2,若點O在△ABC的內部,求證:AB=AC;
(3)若點O在△ABC的外部,AB=AC成立嗎?請畫圖表示.
23.(本題滿分l2分)
某市組織l0輛汽車裝運完A、B、C三種不同品質的橘子共l00噸到外地銷售,按計劃l0輛汽車都要裝滿,且每輛汽車只能裝同一種橘子,根據下表提供的信息,解答以下問題:
橘子品種
A
B
C
每輛汽車云載量(噸)
12
10
8
每噸橘子獲利(千元)
3
4
2
(1)設裝運A種橘子的車輛數為x,裝運B種橘子的車輛數為y,求與x之間的函數關系式;
(2)如果裝運每種橘子的車輛數都不少于2輛,那么車輛的安排方案有幾種?并寫出每種安排方案;
(3)若要使此次銷售獲利最大,應采用哪種安排方案?并求出最大利潤的值.
24.(本題滿分l0分)
實驗與探究:
如圖,在平面直角坐標系中,直線 是第一、三象限的角平分線.
是第一、三象限的角平分線.
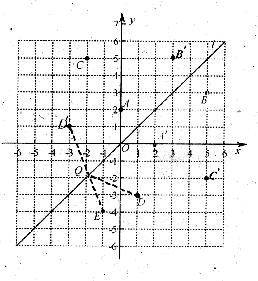
(1)由圖觀察易知A(0,2)關于直線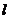 的對稱點A′的坐標為(2,0),請在圖中分別標明B(5,3)、C(-2,5)關于直線的對稱點B′、C′的位置,并寫出他們的坐標:
的對稱點A′的坐標為(2,0),請在圖中分別標明B(5,3)、C(-2,5)關于直線的對稱點B′、C′的位置,并寫出他們的坐標:
B′_______________、C′_________________;
歸納與發現:
運用與拓廣:
(2)結合圖形觀察以上三組點的坐標,你會發現:坐標平面內任一點P(a,6)關于第一、三象限的角平分線的對稱點P′的坐標為____________(不必證明);
(3)已知兩點D(1,-3)、E(-1,-4),試在直線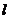 上確定一點Q,使點Q到D、E兩點的距離之和最小,并求出Q點坐標.
上確定一點Q,使點Q到D、E兩點的距離之和最小,并求出Q點坐標.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com