
2008年貴陽市中考模擬試卷十
數 學
一、選擇題(以下每小題都有A、B、C、D四個選項,其中只有一個選項正確。請把正確選項的字母選入該題的括號內。每小題4分,共20分)
1.“太陽能”是一種既無污染又節省地下能源的能量,據科學家統計,平均每平方千米的地面一年從太陽獲得的能量,相當于燃燒130000000千克的煤所產生的能量,用科學記數法表示這個數是( )千克.
A.1.3×108 B.13×107 C.0.13×109 D.1.3×109
2.下列調查工作需采用普查方式的是( ).
A.環保部門對淮河某段水域的水污染情況的調查
B.電視臺對正在播出的某電視節目收視率的調查
C.質檢部門對各廠家生產的電池使用壽命的調查
D.企業在給職工做工作服前進行尺寸大小調查
3.小明根據鄰居家的故事寫了一首小詩:“兒子學成今日返,老父早早到車站,兒子到后細端詳,父子高興把家還.”如果用縱軸y表示父親與兒子行進中離家的距離,用橫軸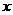 表示父親離家的時間,那么下面的圖像與上述詩的含義大致吻合的是( ).
表示父親離家的時間,那么下面的圖像與上述詩的含義大致吻合的是( ).
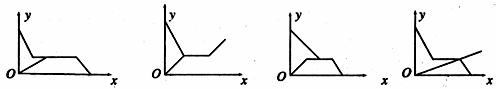
A B C D
4.桌上擺著一個由若干個相同正方體組成的幾何體,其主視圖和左視圖如圖所示,這個幾何體最多可以由( )個這樣的正方體組成.
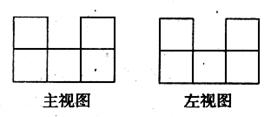
A.11 B.12 C.13 D.14
5.在拼圖游戲中,從下圖(1)的四張紙片中,任取兩張紙片,能拼成“小房子”如(2)的概率等于( ).
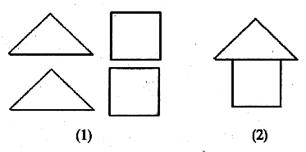
A.l B.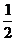 C.
C. D.
D.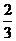
二、填空題(每小題3分,共30分)
6.計算:(一3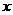 2
2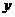 )?(
)?(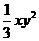 )=_____________.
)=_____________.
7.分解因式: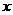 2―9=___________.
2―9=___________.
8.寫出一個圖像經過點(1,一1)的函數表達式__________.
9.如圖,是某希望中學學生選擇棋類、武術、攝影、刺繡四門校本課程情況的扇形統計圖.從圖中可以看出選擇刺繡的學生為__________人.
 ’
’
10.如圖,在數軸上點A和B之間表示整數的點有__________個.
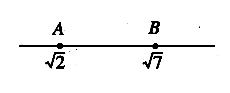
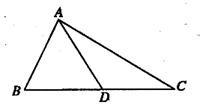
11.如圖,在△ABC中,點D是BC上一點,∠BAD=80°,AB=AD=DC,則∠C=______度.
12.關于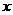 的一元二次方程
的一元二次方程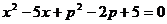 的一個根為1,則實數
的一個根為1,則實數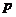 的值是_____.
的值是_____.
13.如圖所示的兩個圓盤中,指針落在每一個數上的機會均等,那么兩個指針同時落在偶數上的概率是____________。
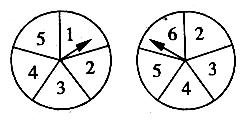
14.小敏在校運動會跳遠比賽中跳出了滿意一跳,函數h=3.5t一4.9t2(t的單位:s,h的單位:m)可以描述他跳躍時重心高度的變化,則他起跳后到重心最高時所用的時間是_________s.
15.如圖,四邊形OABC為菱形,點B、C在以點O為圓心的EF弧上,若OA=3,∠FOC=∠AOE,則扇形DEF的面積為_________。

三.解答題
16.(本題8分)
有一道題:先化簡,再求值: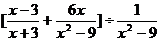 ,其中
,其中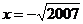 ,小亮同學做題時把
,小亮同學做題時把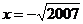 錯抄成了
錯抄成了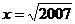 ,但他的計算結果也是正確的,請你解釋這是怎么回事?
,但他的計算結果也是正確的,請你解釋這是怎么回事?
17.(本題10分)
某學校舉行演講比賽,選出了10名同學擔任評委,并事先擬訂從如下4個方案中選擇合理的方案來確定演講者的最后得分(滿分為10分):
方案l:所有評委所給的平均分.
方案2:在所有評委所給的分中,去掉最高分和最低分,然后再計算其余給分的平均數.
方案3:所有評委所給分的中位數.
方案4:所有評委所給分的眾數.
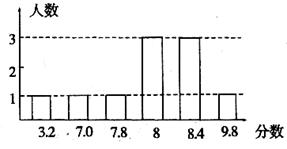
為了探究上述方案的合理性,先對某個同學的演講成績進行了統計實驗,下圖是這個同學的得分統計圖.
(1)分別按上述4個方案計算這個同學演講的最后得分;(8分)
(2)根據(1)中的結果,請用統計的知識說明哪些方案不合適作為這個同學演講的最后得分.(2分)
18.(本題10分):
如圖,已知二次函數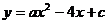 的圖像經過點A和點B.
的圖像經過點A和點B.
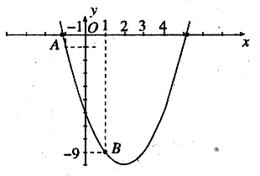
(1)求該二次函數的表達式;(4分)
(2)寫出該拋物線的對稱軸及頂點坐標;(2分)
(3)點P(m,m)與點Q均在該函數圖像上,(其中m>0),且這兩點關于拋物線的對稱軸對稱,求m的值及點Q到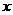 軸的距離.(4分)
軸的距離.(4分)
19.(本題10分)
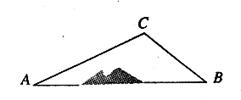
如圖,A、B兩地之間有一座山,汽車原來從A地到B地須經過C地沿折線A―C―B行駛,已知AC=10km,∠A=30°,∠B=45°,則隧道開通后,汽車從A地到B地比原來少走多少千米?(結果精確到0.1km)
20.(本題10分)
將背面相同,正面分別標有數字1、2、3、4的四張卡片洗勻后,背面朝上放在桌面上.
(1)從中隨機抽取一張卡片,求該卡片正面朝上的數字是偶數的概率;(5分)
(2)先從中隨機抽取一張卡片(不放回),將該卡片正面上的數字作為十位上的數字;再隨機抽取一張,將該卡片正面上的數字作為個位上的數字,則組成的兩位數恰好是4的倍數的概率是多少?請用樹狀圖或列表法加以說明.(5分)
21.(本題10分)
甲、乙兩人騎自行車前往A地,他們距A地的路程s(km)與行駛時間t(h)之間的關系如圖所示,請根據圖像所提供的信息解答下列問題:
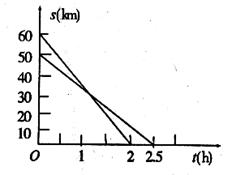
(1)甲、乙兩人的速度各是多少?(4分)
(2)寫出甲、乙兩人距A地的路程s與行駛時間I之間的函數關系式(任寫一個);(3分)
(3)在什么時間內乙比甲離A地更近?(3分)
22.(本題10分)
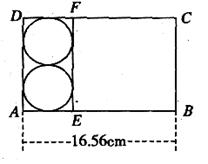
工廠用長方形的鐵皮制作易拉罐,一張長方形鐵皮根據下圖中的數據下料,假設焊接的部分忽略不計,求這個易拉罐的容積.(取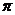 =3.14,精確到0.01立方米)
=3.14,精確到0.01立方米)
23.(本題12分)
如圖,已知在梯形ABCD中,AD//BC,AB=DC,對角線AC和BD相交于點D,E是BC邊上一個動點(層點不與B、C兩點重合),EF//BD交AC于點F,EG//AC交BD于點G

(1)求證:四邊形EFOG的周長等于2OB;(6分)
(2)請你將上述題目的條件“梯形ABCD中,AD//BC,AB=DC”改為另一種四邊形,其他條件不變,使得結論“四邊形EFOG的周長等于2OB”仍成立,并將改編后的題目寫出已知和求證.但不證明.(6分)
24.(本題10分)
某水果批發商銷售每箱進價為40元的蘋果,物價部門規定每箱售價不得高于55元,市場調查發現,若每箱以50元的價格出售,平均每天銷售90箱,價格每提高1元,平均每天少銷售3箱.
(1)求平均每天銷售量y(箱)與銷售價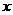 (元/箱)之間的函數關系式;(3分)
(元/箱)之間的函數關系式;(3分)
(2)求平均每天的銷售利潤w(元)與銷售價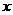 (元/箱)之間的函數關系式;(3分)
(元/箱)之間的函數關系式;(3分)
(3)當每箱蘋果的銷售價為多少時,可以獲得最大利潤?最大利潤是多少?(4分)
25.(本題10分l
兩條平行直線上各有n個點,用這n對點按如下規則連接線段:
①平行線之間的點在連線段時,可以有共同的端點,但不能有其他交點;
②符合①要求的線段須全部畫出.
圖(1)展示了當n=1時的情況,此時圖中三角形的個數為0;
圖(2)展示了當n=2時的情況,此時圖中三角形的個數為2.
(1)當n=3時,請在圖(3)中畫出使三角形個數最少的圖形,此時圖中三角形的個數為___________.(5分)
(2)試猜想當有n對點時,按上述規則畫出的圖形中,最少有多少個三角形?(3分)
(3)當n=2008時,按上述規則畫出的圖形中,最少有多少個三角形?(2分)

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com