
湖南省“三市七校”2007屆畢業班第二次聯考試題卷數學(理科)
命題者:南縣一中:陳敬波、沅江一中:朱清明、長煉中學:吳湘波.
考試時量:120分鐘,試卷滿分:150分.
 參考公式:
參考公式:
一、選擇題:本大題共10小題,每小題5分,共50分,在每小題給出的四個選項中,只有一項是符合題目要求的.
1.已知全集U = {1,2,3,4,5,6,7},A = {3,4,5},B = {1,3,6},則A∩(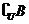 )等于 ( )
)等于 ( )
A.{4,5} B.{2,4,5,7}
C.{1,6} D.{3}
2. 若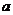 、
、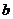 是兩條不重合直線,
是兩條不重合直線,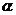 、
、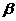 是兩個不重合的平面,則
是兩個不重合的平面,則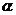 ∥
∥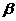 的一個充分而不必要條件是( )
的一個充分而不必要條件是( )
(A)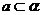 ,
,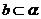 ,
,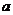 ∥
∥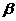 且b∥
且b∥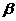 (B)
(B)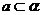 ,
,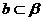 ,且a∥b
,且a∥b
(C)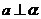 ,
,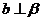 ,且
,且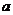 ∥
∥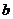 (D)
(D)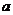 ∥
∥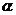 ,
,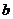 ∥
∥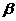 ,且a∥b
,且a∥b
3. 在等差數列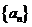 中,
中, ,
,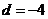 ,若
,若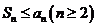 ,則
,則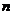 的最小值為( )
的最小值為( )
(A)60 (B)62 (C)70 (D)72
4. 已知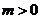 ,
,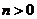 ,且滿足
,且滿足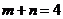 ,則下列不等式恒成立的是( )
,則下列不等式恒成立的是( )
(A)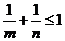 (B)
(B) (C)
(C)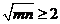 (D)
(D)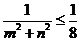
5.以直線y= -x+1與坐標軸的交點為焦點的拋物線的標準方程為( )
A x2=4y或y2=4x B x2=2y或y2=2x
C x2=-4y或y2=-4x D x2=2y或y2=-2x
6.定義:| a × b
| = | a | | b | sin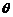 ,其中
,其中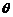 為向量a與b的夾角,若| a | = 2,| b | = 5,a ? b = ? 6,則| a
× b | =( )
為向量a與b的夾角,若| a | = 2,| b | = 5,a ? b = ? 6,則| a
× b | =( )
A.-8 B.
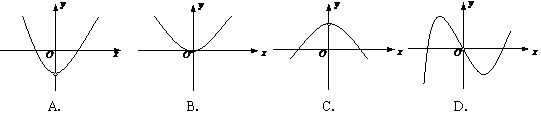
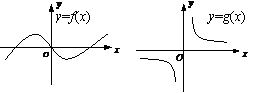 7.已知
7.已知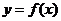 與
與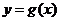 的圖象如圖所示,
的圖象如圖所示,
則函數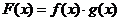 的圖象可以是
的圖象可以是
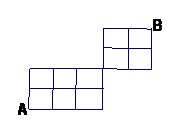
8.在某城市中,A、B兩地有如右圖所示道路網,從A地到B地最近的走法有( )種
A 25 B 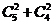 C
C 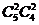 D
D 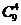
9.一個三棱錐S-ABC的三條側棱SA、SB、SC兩兩互相垂直,且長度分別為1,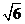 ,3,則這個三棱錐的外接球的表面積為( )
,3,則這個三棱錐的外接球的表面積為( )
(A) 16π (B) 32π (C) 36π (D) 64π
10.定義在R上的函數f(x),給出下列四個命題:
① 若f(x)是偶函數,則f(x+3)的圖象關于直線x=-3對稱;
② 若f(x+3)=-f(3-x),則f(x)的圖象關于點(3,0)對稱;
③ 若f(x+3)是偶函數,則f(x)的圖象關于直線x=3對稱;
④ y=f(x+3)與y=f(3-x)的圖象關于直線x=3對稱.
其中正確命題的個數有( )
A 0 B 1 C 2 D 3
試題卷 第 Ⅱ 卷 (非選擇題,共100分)
二、填空題:本大題共5小題,每小題5分,共25分。將正確答案填在答題卷上對應題號的橫線上。
11.設i是虛數單位,則 的虛部為 。
的虛部為 。
12. 已知變量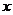 、
、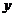 滿足
滿足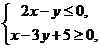 則
則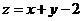 的最大值為__________。
的最大值為__________。
13.若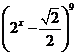 的展開式的第7項為
的展開式的第7項為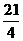 ,則
,則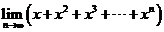

14. 已知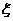 服從正態分布N(5,4),那么P(
服從正態分布N(5,4),那么P(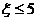 )=____________.
)=____________.
15. 對于一切實數x,令[x]為不大于x的最大整數,則函數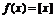 稱為高斯函數或取整函數,如 f(2.1)=2;若
稱為高斯函數或取整函數,如 f(2.1)=2;若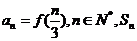 為數列
為數列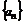 的前n項和,則
的前n項和,則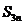 =____________.
=____________.
三、解答題:本大題共6小題,滿分80分。解答應寫出文字說明,證明過程或演算步驟。
16.(本大題滿分12分)
已知銳角△ABC中,三個內角為A、B、C,兩向量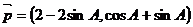 ,
,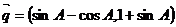 ,若
,若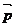 與
與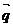 是共線向量,(1)∠A的大小;(2)求函數
是共線向量,(1)∠A的大小;(2)求函數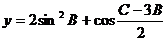 取最大值時,∠B的大小
取最大值時,∠B的大小
17. (本大題滿分13分)
有A,B,C,D四個城市,它們都有一個著名的旅游點依此記為a,b,c,d把A,B,C,D和a,b,c,d分別寫成左、右兩列,現在一名旅游愛好者隨機用4條線把左右全部連接起來,構成“一一對應”,已知連接一個城市與該城市的旅游點正確的得2分,連錯的得0分;
(1)求該愛好者至少得2分的概率; (2)求所得分的數學期望?
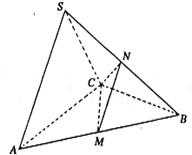 18.(本大題滿分13分) 在三棱錐S―ABC中,△ABC是邊長為4的正三角形,平面SAC⊥平面ABC,SA=SC=2
18.(本大題滿分13分) 在三棱錐S―ABC中,△ABC是邊長為4的正三角形,平面SAC⊥平面ABC,SA=SC=2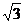 ,M、N分別為AB、SB的中點.
,M、N分別為AB、SB的中點.
(1)證明:AC⊥SB;
(2)求二面角N―CM―B的大小;
(3)求點B到平面CMN的距離.
19.(本大題滿分14分)
通過研究學生的學習行為,專家發現,學生的注意力隨著老師講課時間的變化而變化,講課開始時,學生的興趣激增;中間有一段時間,學生的興趣保持較理想的狀態,隨后學生的注意力開始分散,設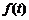 表示學生注意力隨時間t (分鐘)的變化規律(
表示學生注意力隨時間t (分鐘)的變化規律(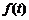 越大,表明學生注意力越集中),經過實驗分析得知:
越大,表明學生注意力越集中),經過實驗分析得知:
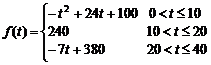
(1)講課開始后多少分鐘,學生的注意力最集中?能持續多少分鐘?
(2)講課開始后5分鐘與講課開始后25分鐘比較,何時學生的注意力更集中?
(3)一道數學難題,需要講解24分鐘,并且要求學生的注意力至少達到180,那么經過
適當安排,老師能否在學生達到所需的狀態下講授完這道題目?
20.(本大題滿分14分)
已知橢圓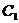 :
: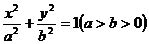 的左、右焦點分別為
的左、右焦點分別為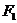 ,
,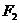 ,右頂點為A,P是橢圓
,右頂點為A,P是橢圓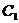 上任意一點,設該雙曲線
上任意一點,設該雙曲線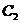 :以橢圓
:以橢圓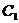 的焦點為頂點,頂點為焦點,B是雙曲線
的焦點為頂點,頂點為焦點,B是雙曲線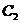 在第一象限內的任意一點,且
在第一象限內的任意一點,且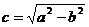 。
。
(1)設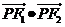 的最大值為
的最大值為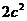 ,求橢圓離心率;(2)若橢圓離心率
,求橢圓離心率;(2)若橢圓離心率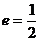 時,證明:總有
時,證明:總有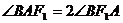 成立。
成立。
21.(本大題滿分14分)
已知函數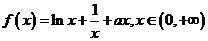 (a為實常數).
(a為實常數).
(1) 當a = 0時,求 的最小值;
的最小值;
(2)若 在
在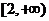 上是單調函數,求a的取值范圍;
上是單調函數,求a的取值范圍;
(3)設各項為正的無窮數列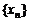 滿足
滿足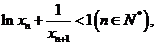 證明:
證明: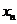 ≤1(n∈N*).
≤1(n∈N*).
一.1、A,2、C,3、B,4、D,5、C,6、B,7、A,8、C,9、A,10、D
二.11、-3;.12、1;13、 14、
14、 15、
15、
三.16.解:
 ……(2’)
……(2’)
整理得: ……………………………(4’)
……………………………(4’)
又A為銳角, …………………(6’)
…………………(6’)
(2)由(1)知 ………………………(7’)
………………………(7’)
故

……………………………(12’)
當B=600時,Y取得最大值。……………………(13’)
17. 設答對題的個數為y,得分為 ,y=0,1,2,4 ,
,y=0,1,2,4 , =0,2,4,8………(1’)
=0,2,4,8………(1’)
∵ ,
,
 ,
,