日本成人片在线_久久免费精品视频_国产午夜精品久久久久久免费视_校花撩起jk露出白色内裤国产精品_av影片免费在线观看_国产小视频在线看_最新av免费在线观看_99久久99久久精品国产片_欧美成人猛片aaaaaaa_蜜桃免费网站一区二区三区

（1）求出列聯表中字母x、y、m、n的值；

（2）①從此樣本中，對單車用戶按年齡采取分層抽樣的方法抽出5人進行深入調研，其中不小于40歲的人應抽多少人？

②從獨立性檢驗角度分析，能否有以上的把握認為該市成人市民是否為單車用戶與年齡是否小于40歲有關.

下面臨界值表供參考：

【題目】已知函數是定義在R上的奇函數，當時，，給出下列命題：

①當時，；

②函數有2個零點；

③的解集為；

④，，都有.

其中真命題的個數為（ ）

A.4B.3C.2D.1

【題目】中國古代儒家要求學生掌握六種基本才藝：禮、樂、射、御、書、數，簡稱“六藝”,某高中學校為弘揚“六藝”的傳統文化，分別進行了主題為“禮、樂、射、御、書、數”六場傳統文化知識競賽，現有甲、乙、丙三位選手進入了前三名的最后角逐,規定：每場知識競賽前三名的得分都分別為且；選手最后得分為各場得分之和，在六場比賽后，已知甲最后得分為分，乙和丙最后得分都是分，且乙在其中一場比賽中獲得第一名，下列說法正確的是( )

A. 乙有四場比賽獲得第三名

B. 每場比賽第一名得分為

C. 甲可能有一場比賽獲得第二名

D. 丙可能有一場比賽獲得第一名

【題目】某籃球隊員進行定點投籃訓練，每次投中的概率是，且每次投籃的結果互不影響.

（1）假設這名隊員投籃5次，求恰有2次投中的概率；

（2）假設這名隊員投籃3次，每次投籃，投中得1分，為投中得0分，在3次投籃中，若有2次連續投中，而另外一次未投中，則額外加1分；若3次全投中，則額外加3分，記為隊員投籃3次后的總的分數，求的分布列及期望.

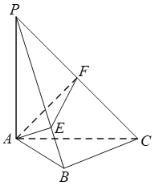
【題目】在《九章算術》中，將四個面都為直角三角形的四面體稱之為鱉臑.如圖，在鱉臑中，平面，，且，過點分別作于點，于點，連結，當的面積最大時，__________.

【題目】如圖，在四棱錐中，底面，，，，，點為棱的中點

（1）證明：；

（2）若為棱上一點，滿足，求銳二面角的余弦值.

【題目】已知橢圓右焦點，離心率為，過作兩條互相垂直的弦，設中點分別為．

(1) 求橢圓的標準方程；

(2)求以為頂點的四邊形的面積的取值范圍；

【題目】在平面直角坐標系xy中，曲線C的參數方程為為參數），在以為極點，軸的非負半軸為極軸的極坐標系中，直線的極坐標方程為。

（1）求曲線C的極坐標方程；

（2）設直線與曲線C相交于A，B兩點，P為曲C上的一動點，求△PAB面積的最大值.

（1）求f（x）＝sinx（x∈R），g（x）＝cosx（x∈R）的差距；

（2）設f（x）＝（x∈[1,]），g（x）＝mlnx （x∈[1,]）．（e≈2.718）

①若m＝2，且||f（x），g（x）||＝1，求滿足條件的最大正整數a；

②若a＝2，且||f（x），g（x）||＝2，求實數m的取值范圍．

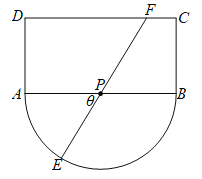
【題目】如城某觀光區的平面示意圖如圖所示，其中矩形的長千米，寬千米，半圓的圓心為中點.為了便于游客觀光休閑，在觀光區鋪設一條由圓弧、線段、組成的觀光道路.其中線段經過圓心，且點在線段上（不含線段端點、）.已知道路、的造價為元每千米，道路造價為元每千米，設，觀光道路的總造價為.

（1）試求與的函數關系式：；

（2）當為何值時，觀光道路的總造價最小.