
【題目】設△ABC的三內角A、B、C的對邊分別是a、b、c,且b(sinB﹣sinC)+(c﹣a)(sinA+sinC)=0 (Ⅰ)求角A的大小;
(Ⅱ)若a= ![]() ,sinC=
,sinC= ![]() sinB,求△ABC的面積.
sinB,求△ABC的面積.
【答案】解:(Ⅰ)因為b(sinB﹣sinC)+(c﹣a)(sinA+sinC)=0, 由正弦定理得b(b﹣a)+(c﹣a)(a+c)=0,∴b2+c2﹣a2=bc,
∴由余弦定理得 ![]() ,∴在△ABC中,
,∴在△ABC中, ![]() .
.
(Ⅱ)方法一:因為 ![]() ,且
,且 ![]() ,∴
,∴ ![]()
∴ ![]() ,∴tanB=1,在△ABC中,
,∴tanB=1,在△ABC中, ![]()
又在△ABC中,由正弦定理得 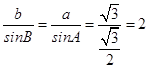 ,∴
,∴ ![]()
∴△ABC的面積 ![]()
方法二:因為 ![]() ,由正弦定理得
,由正弦定理得 ![]()
而 ![]() ,
, ![]() ,由余弦定理得b2+c2﹣bc=a2 , ∴
,由余弦定理得b2+c2﹣bc=a2 , ∴ 
∴b2=2,即 ![]() ,
, ![]()
∴△ABC的面積S= ![]() =
= ![]()
【解析】(Ⅰ)由正弦定理得b2+c2﹣a2=bc,由由余弦定理求角A的大小;(Ⅱ)若a= ![]() ,sinC=
,sinC= ![]() sinB,利用三角形的面積公式,即可求△ABC的面積.
sinB,利用三角形的面積公式,即可求△ABC的面積.


科目:高中數學 來源: 題型:
【題目】設函數f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的導函數.
(1)g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+ , 求g1(x),g2(x),g3(x),并猜想gn(x)的表達式(不必證明);
(2)若f(x)≥ag(x)恒成立,求實數a的取值范圍;
(3)設n∈N+ , 比較g(1)+g(2)+…+g(n)與n﹣f(n)的大小,并用數學歸納法加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)是定義在R上的可導函數,且滿足(x﹣1)f′(x)≥0,則必有( )
A.f(0)+f(2)<2f(1)
B.f(0)+f(2)>2f(1)
C.f(0)+f(2)≤2f(1)
D.f(0)+f(2)≥2f(1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義域為R的偶函數f(x)滿足對x∈R,有f(x+2)=f(x)﹣f(1),且當x∈[2,3]時,f(x)=﹣2x2+12x﹣18,若函數y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三個零點,則a的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解今年某校高三畢業班準備報考飛行員學生的體重情況,將所得的數據整理后,畫出了頻率分布直方圖(如圖),已知圖中從左到右的前3個小組的頻率之比為1:2:3,其中第2小組的頻數為15.
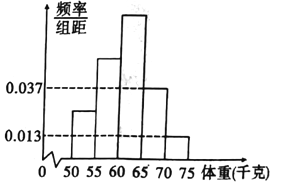
(1)求該校報考飛行員的總人數;
(2)以這所學校的樣本數據來估計全省的總體數據,若從全省報考飛行員的同學中(人數很多)任選三人,設![]() 表示體重超過65公斤的學生人數,求
表示體重超過65公斤的學生人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)若函數![]() 在
在![]() 處的切線平行于直線
處的切線平行于直線![]() ,求實數a的值;
,求實數a的值;
(Ⅱ)判斷函數![]() 在區間
在區間![]() 上零點的個數;
上零點的個數;
(Ⅲ)在(Ⅰ)的條件下,若在![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com