
在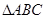 中,角
中,角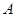 、
、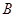 、
、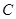 的對邊分別為
的對邊分別為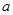 、
、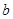 、
、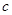 ,且滿足
,且滿足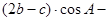

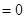 。
。
(1)求角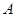 的大小;
的大小;
(2)若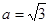 ,
,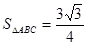 ,試判斷
,試判斷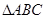 的形狀,并說明理由
的形狀,并說明理由
(1)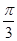 (2)等邊三角形
(2)等邊三角形
【解析】本試題主要考查了解三角形的運用。
解:(1)法一:∵(2b-c)cosA-acosC=0,
由正弦定理得,(2sinB-sinC)cosA-sinAcosC=0,
∴2sinBcosA-sin(A+C)=0,即sinB(2cosA-1)=0.∵0<B<π,∴sinB≠0,∴cosA=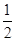 .
.
∵0<A<π,∴A=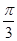 .
.
法二:∵(2b-c)cosA-acosC=0,由余弦定理得,(2b-c)·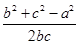 -a·
-a·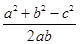 =0,整理得b2+c2-a2=bc,∴cosA=
=0,整理得b2+c2-a2=bc,∴cosA=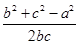 =
=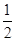 .∵0<A<π,∴A=
.∵0<A<π,∴A=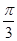 .
.
(2)∵S△ABC=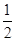 bcsinA=
bcsinA=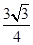 ,即bcsin
,即bcsin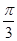 =
=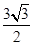 ,
,
∴bc=3,①∵a2=b2+c2-2bccosA,∴b2+c2=6,②
由①②得b=c=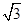 ,∴△ABC為等邊三角形.
,∴△ABC為等邊三角形.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2012-2013學年安徽省高三第一次質量檢測理科數學試卷(解析版) 題型:解答題
(本小題滿分12分)
已知函數
 的圖象過點
的圖象過點 .
.
(Ⅰ)求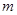 的值;
的值;
(Ⅱ)在△ 中,角
中,角 ,
, ,
, 的對邊分別是
的對邊分別是 ,
, ,
, .若
.若 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年北京市朝陽區高考二模理科數學試卷(解析版) 題型:解答題
(本小題滿分13分)
已知函數
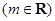 的圖象過點
的圖象過點 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)在△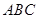 中,角
中,角 ,
, ,
, 的對邊分別是
的對邊分別是 ,
, ,
, .若
.若 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010屆漳州一中高三(上)理科數學期末測試卷 題型:解答題
(本小題滿分12分)已知 ,函數
,函數 的最小正周期為
的最小正周期為 ,且當
,且當 時,
時, 的最小值為0.
的最小值為0.
(1)求 和
和 的值;
的值;
(2)在 中,角
中,角 、
、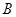 、
、 的對邊分別是
的對邊分別是 、
、 、
、 ,滿足
,滿足 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com