
已知數列![]() 滿足遞推關系式:
滿足遞推關系式:![]() ,
,![]() .
.
(1)若![]() ,證明:(ⅰ)當
,證明:(ⅰ)當![]() 時,有
時,有![]() ;(ⅱ)當
;(ⅱ)當![]() 時,有
時,有![]() .
.
(2)若![]() ,證明:當
,證明:當![]() 時,有
時,有![]() .
.
證明略
因為![]() ,故
,故![]() ,即數列
,即數列![]() 為遞增數列.
為遞增數列.
(1)(ⅰ)由![]() 及
及![]() 可求得
可求得![]() ,于是當
,于是當![]() 時,
時,![]() ,于是
,于是![]() ,即當
,即當![]() 時,
時,![]() .
.
…………………………5分
(ⅱ)由于![]() 時,
時,![]() ,所以
,所以![]() 時,
時,![]() .
.
由![]() 可得
可得![]() .
.
先用數學歸納法證明下面的不等式成立:![]() (
(![]() ).
).
Ⅰ)當![]() 時,
時,![]() ,結論成立.
,結論成立.
Ⅱ)假設結論對![]() 成立,即
成立,即![]() ,則結合(ⅰ)的結論可得
,則結合(ⅰ)的結論可得
![]() ,即當
,即當![]() 時結論也成立.
時結論也成立.
綜合Ⅰ),Ⅱ)可知,不等式![]() 對一切
對一切![]() 都成立.
都成立.
因此,當![]() 時,
時,![]()
![]() ,即
,即![]() .
.
又![]() ,
,![]() ,所以當
,所以當![]() 時,有
時,有![]() .
.
…………………………10分
(2)由于![]() ,而數列
,而數列![]() 為遞增數列,故當
為遞增數列,故當![]() 時,有
時,有![]() .
.
由![]() 可得
可得![]() ,而
,而![]() ,于是
,于是
![]() .
.
下面先證明:當![]() 時,有
時,有![]() (*)
(*)
Ⅰ)根據![]() 及
及![]() 計算易得
計算易得![]() ,
,
![]() ,而
,而![]() ,
,
故![]() ,即當
,即當![]() 時,結論成立.
時,結論成立.
Ⅱ)假設結論對![]() 成立,即
成立,即![]() .
.
因為![]() ,而函數
,而函數![]() 在
在![]() 時為增函數,所以
時為增函數,所以
![]() ,
,
即當![]() 時結論也成立.
時結論也成立.
綜合Ⅰ),Ⅱ)可知,不等式![]() 對一切
對一切![]() 都成立.
都成立.
于是當![]() 時,
時,![]() ,故
,故![]() ,所以
,所以![]() .
.
…………………………20分


 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:高中數學 來源: 題型:
2
| ||
| an+1 |
| 1 |
| a1+1 |
| 1 |
| a2+1 |
| 1 |
| an+1 |
| 1 |
| 2n |
查看答案和解析>>
科目:高中數學 來源:2010-2011學年湖北省武漢二中、龍泉中學高一下學期期末聯考數學 題型:解答題
(14分)已知數列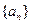 滿足遞推關系,
滿足遞推關系,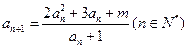 ,又
,又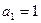
(1)當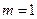 時,求
時,求 證數列
證數列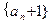 為等比數列;
為等比數列;


(2)當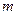 在什么范圍內取值時,能使數列
在什么范圍內取值時,能使數列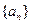 滿足不等式
滿足不等式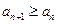 恒成立?
恒成立?
(3)當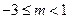 時,證明:
時,證明: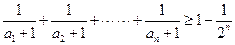 .
.
查看答案和解析>>
科目:高中數學 來源:2013屆湖北省高一下學期期末聯考數學 題型:解答題
(14分)已知數列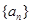 滿足遞推關系,
滿足遞推關系,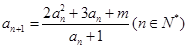 ,又
,又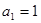
(1)當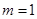 時,求證數列
時,求證數列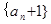 為等比數列;
為等比數列;

(2)當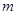 在什么范圍內取值時,能使數列
在什么范圍內取值時,能使數列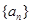 滿足不等式
滿足不等式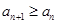 恒成立?
恒成立?
(3)當 時,證明:
時,證明: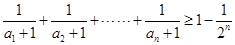 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com