【題目】袋子中有四個小球，分別寫有“四”“校”“聯”“考”四個字，有放回地從中任取一個小球，取到“聯”就停止，用隨機模擬的方法估計直到第二次停止的概率：先由計算器產生1到4之間取整數值的隨機數，且用1，2，3，4表示取出小球上分別寫有“四”“校”“聯”“考”四個字，以每兩個隨機數為一組，代表兩次的結果，經隨機模擬產生了20組隨機數：13 24 12 32 43 14 24 32 31 21 23 13 32 21 24 42 13 32 23 34據此估計，直到第二次就停止的概率為______.
新課標快樂提優暑假作業陜西旅游出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案科目：高中數學 來源： 題型：
【題目】為了了解手機品牌的選擇是否和年齡的大小有關，隨機抽取部分華為手機使用者和蘋果機使用者進行統計，統計結果如下表：
年齡 手機品牌 | 華為 | 蘋果 | 合計 |
30歲以上 | 40 | 20 | 60 |
30歲以下（含30歲） | 15 | 25 | 40 |
合計 | 55 | 45 | 100 |
附：
P（ | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
根據表格計算得
的觀測值
，據此判斷下列結論正確的是（ ）
A.沒有任何把握認為“手機品牌的選擇與年齡大小有關”
B.可以在犯錯誤的概率不超過0.001的前提下認為“手機品牌的選擇與年齡大小有關”
C.可以在犯錯誤的概率不超過0.01的前提下認為“手機品牌的選擇與年齡大小有關”
D.可以在犯錯誤的概率不超過0.01
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
，函數
的圖象在點
處的切線平行于
軸．
（Ⅰ）求
的值
（Ⅱ）設
，若
的所有零點中，僅有兩個大于
，設為
，
（
）
（1）求證：
，
．
（2）過點
，
的直線的斜率為
，證明：
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】直線l過曲線C：y
x2的焦點F，并與曲線C交于A（x1，y1），B（x2，y2）兩點．
（1）求證：x1x2＝﹣16；
（2）曲線C分別在點A，B處的切線（與C只有一個公共點，且C在其一側的直線）交于點M，求點M的軌跡．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
（
）的左右焦點分別為
，
，點
為短軸的一個端點，
.
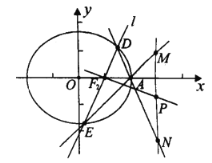
（1）求橢圓C的方程；
（2）如圖，過右焦點，且斜率為k（
）的直線l與橢圓C相交于D，E兩點，A為橢圓的右頂點，直線
，
分別交直線
于點M，N，線段
的中點為P，記直線
的斜率為
.試問
是否為定值？若為定值，求出該定值；若不為定值，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校100名學生期中考試語文成績的頻率分布直方圖如圖所示，其中成績分組區間是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．
(1)求圖中a的值；
(2)根據頻率分布直方圖，估計這100名學生語文成績的平均分；
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如下表所示，求數學成績在[50,90)之外的人數.
分數段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為
（
為參數）．
是曲線上的動點，將線段
繞
點順時針旋轉
得到線段
，設點
的軌跡為曲線
．以坐標原點為極點，
軸正半軸為極軸建立極坐標系．
（I）求曲線，的極坐標方程；
（II）在（I）的條件下，若射線
與曲線，分別交于
兩點（除極點外），且有定點
，求
面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
