【題目】斜率為2的直線l在雙曲線
上截得的弦長為
，求l的方程．
【答案】y＝2x±
【解析】
設直線
的方程為
,設和雙曲線的兩交點為
，將直線方程代入雙曲線方程可得到關于
的一元二次方程，根據韋達定理可用
表示
,然后求弦長等于
,這樣可得到關于的方程，解方程即得的值，從而便求出來直線的方程.
設直線l的方程為y＝2x＋m，
由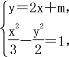
得10x2＋12mx＋3(m2＋2)＝0.(*)
設直線l與雙曲線交于A(x1，y1)，B(x2，y2)兩點，由根與系數的關系，
得x1＋x2＝－
m，x1x2＝
(m2＋2)．
∴|AB|2＝(x1－x2)2＋(y1－y2)2＝5(x1－x2)2＝5[(x1＋x2)2－4x1x2]＝5
.∵|AB|＝
，∴
m2－6(m2＋2)＝6，∴m2＝15，m＝±
.
由(*)式得Δ＝24m2－240，
把m＝±代入上式，得Δ>0，∴m的值為±，
∴所求l的方程為y＝2x±.
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C所對的邊分別為a，b，c且滿足csinA=acosC，
（1）求角C的大小；
（2）求 
sinA﹣cos（B+ 
）的最大值，并求取得最大值時角A，B的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知一個口袋內有4個不同的紅球,6個不同的白球.
(1)從中任取4個球,紅球的個數不比白球的個數少的取法有多少種?
(2)從中任取5個球,記取到紅球的個數為X,求X的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）=axn（1﹣x）（x＞0，n∈N*），當n=﹣2時，f（x）的極大值為 
．
（1）求a的值；
（2）求證：f（x）+lnx≤0；
（3）求證：f（x）＜ 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線y2=8x的準線與雙曲線 
﹣ 
=1（a＞0，b＞0）相交于A、B兩點，雙曲線的一條漸近線方程是y= 
x，點F是拋物線的焦點，且△FAB是等邊三角形，則該雙曲線的標準方程是（ ）
A.
﹣ 
=1
B.
﹣ 
=1
C.
﹣ 
=1
D.
﹣ 
=1
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P﹣ABCD中，底面ABCD為矩形，PA⊥平面ABCD，E為PD的中點．
（1）證明：PB∥平面AEC；
（2）已知AP=AB=1，AD= 
，求二面角D﹣AE﹣C的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題p:函數f(x)=|2x+3c|在[-1,+∞)上單調遞增;命題q:函數g(x)=
+2有零點.
(1)若命題p和q均為真命題,求實數c的取值范圍;
(2)是否存在實數c,使得p∧(q)是真命題?若存在,求出c的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動點M（x，y）到直線ι：x=4的距離是它到點N（1，0）的距離的2倍．
（1）求動點M的軌跡C的方程；
（2）過點P（0，3）的直線m與軌跡C交于A，B兩點，若A是PB的中點，求點A的坐標．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
