
【題目】如圖,在四棱錐P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(12分) 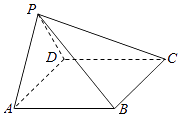
(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.
【答案】
(1)證明:∵∠BAP=∠CDP=90°,∴PA⊥AB,PD⊥CD,
∵AB∥CD,∴AB⊥PD,
又∵PA∩PD=P,且PA平面PAD,PD平面PAD,
∴AB⊥平面PAD,又AB平面PAB,
∴平面PAB⊥平面PAD;
(2)解:∵AB∥CD,AB=CD,∴四邊形ABCD為平行四邊形,
由(1)知AB⊥平面PAD,∴AB⊥AD,則四邊形ABCD為矩形,
在△APD中,由PA=PD,∠APD=90°,可得△PAD為等腰直角三角形,
設PA=AB=2a,則AD= ![]() .
.
取AD中點O,BC中點E,連接PO、OE,
以O為坐標原點,分別以OA、OE、OP所在直線為x、y、z軸建立空間直角坐標系,
則:D( ![]() ),B(
),B( ![]() ),P(0,0,
),P(0,0, ![]() ),C(
),C( ![]() ).
).
![]() ,
, ![]() ,
, ![]() .
.
設平面PBC的一個法向量為 ![]() ,
,
由  ,得
,得 ![]() ,取y=1,得
,取y=1,得 ![]() .
.
∵AB⊥平面PAD,AD平面PAD,∴AB⊥AD,
又PD⊥PA,PA∩AB=A,
∴PD⊥平面PAB,則 ![]() 為平面PAB的一個法向量,
為平面PAB的一個法向量, ![]() .
.
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
由圖可知,二面角A﹣PB﹣C為鈍角,
∴二面角A﹣PB﹣C的余弦值為 ![]() .
.

【解析】(1.)由已知可得PA⊥AB,PD⊥CD,再由AB∥CD,得AB⊥PD,利用線面垂直的判定可得AB⊥平面PAD,進一步得到平面PAB⊥平面PAD; (2.)由已知可得四邊形ABCD為平行四邊形,由(1)知AB⊥平面PAD,得到AB⊥AD,則四邊形ABCD為矩形,設PA=AB=2a,則AD= ![]() .取AD中點O,BC中點E,連接PO、OE,以O為坐標原點,分別以OA、OE、OP所在直線為x、y、z軸建立空間直角坐標系,求出平面PBC的一個法向量,再證明PD⊥平面PAB,得
.取AD中點O,BC中點E,連接PO、OE,以O為坐標原點,分別以OA、OE、OP所在直線為x、y、z軸建立空間直角坐標系,求出平面PBC的一個法向量,再證明PD⊥平面PAB,得 ![]() 為平面PAB的一個法向量,由兩法向量所成角的余弦值可得二面角A﹣PB﹣C的余弦值.
為平面PAB的一個法向量,由兩法向量所成角的余弦值可得二面角A﹣PB﹣C的余弦值.
【考點精析】根據(jù)題目的已知條件,利用平面與平面垂直的判定的相關(guān)知識可以得到問題的答案,需要掌握一個平面過另一個平面的垂線,則這兩個平面垂直.


科目:高中數(shù)學 來源: 題型:
【題目】如圖,在三棱錐A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,點E、F(E與A、D不重合)分別在棱AD,BD上,且EF⊥AD. 求證:(Ⅰ)EF∥平面ABC;
(Ⅱ)AD⊥AC.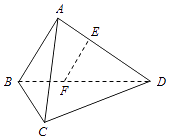
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四面體![]() 中,
中, ![]() 是正三角形,
是正三角形, ![]() 是直角三角形,
是直角三角形, ![]() ,
,![]() .
.
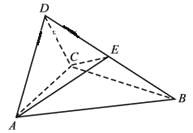
(1)證明:平面![]() 平面
平面![]() ;
;
(2)過![]() 的平面交
的平面交![]() 于點
于點![]() ,若平面
,若平面![]() 把四面體
把四面體![]() 分成體積相等的兩部分,求二面角
分成體積相等的兩部分,求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知圓M過C(1,-1),D(-1,1)兩點,且圓心M在x+y-2=0上.
(1)求圓M的方程;
(2)設點P是直線3x+4y+8=0上的動點,PA,PB是圓M的兩條切線,A,B為切點,求四邊形PAMB面積的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}的前n項和公式為Sn=2n2-30n.
(1)求數(shù)列{an}的通項公式an;(2)求Sn的最小值及對應的n值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖程序框圖是為了求出滿足3n﹣2n>1000的最小偶數(shù)n,那么在 ![]() 和
和 ![]() 兩個空白框中,可以分別填入( )
兩個空白框中,可以分別填入( )
A.A>1000和n=n+1
B.A>1000和n=n+2
C.A≤1000和n=n+1
D.A≤1000和n=n+2
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數(shù)f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.(10分)
(1)當a=1時,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】棱長為1的正方體![]() 中,
中,![]() 分別是
分別是![]() 的中點.
的中點.
①![]() 在直線
在直線![]() 上運動時,三棱錐
上運動時,三棱錐![]() 體積不變;
體積不變;
②![]() 在直線
在直線![]() 上運動時,
上運動時,![]() 始終與平面
始終與平面![]() 平行;
平行;
③平面![]() 平面
平面![]() ;
;
④連接正方體![]() 的任意的兩個頂點形成一條直線,其中與棱
的任意的兩個頂點形成一條直線,其中與棱![]() 所在直線異面的有
所在直線異面的有![]() 條;
條;
其中真命題的編號是_______________.(寫出所有正確命題的編號)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com