
【題目】已知函數 ![]() 是奇函數,f(x)=lg(10x+1)+bx是偶函數.
是奇函數,f(x)=lg(10x+1)+bx是偶函數.
(1)求a和b的值.
(2)說明函數g(x)的單調性;若對任意的t∈[0,+∞),不等式g(t2﹣2t)+g(2t2﹣k)>0恒成立,求實數k的取值范圍.
(3)設 ![]() ,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求實數a的取值范圍.
,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求實數a的取值范圍.
【答案】
(1)解:由g(0)=0得,a=1,
則 ![]() ,
,
經檢驗g(x)是奇函數,
故a=1,
由f(﹣1)=f(1)得,則 ![]() ,
,
故 ![]() ,
,
經檢驗f(x)是偶函數
∴a=1, ![]()
(2)解:∵ ![]() ,且g(x)在(﹣∞,+∞)單調遞增,且g(x)為奇函數.
,且g(x)在(﹣∞,+∞)單調遞增,且g(x)為奇函數.
∴由g(t2﹣2t)+g(2t2﹣k)>0恒成立,
得g(t2﹣2t)>﹣g(2t2﹣k)=g(﹣2t2+k),
∴t2﹣2t>﹣2t2+k,t∈[0,+∞)恒成立
即3t2﹣2t>k,t∈[0,+∞)恒成立
令F(x)=3t2﹣2t,在[0,+∞)的最小值為 ![]()
∴ ![]()
(3)解:h(x)=lg(10x+1),
h(lg(10a+9))=lg[10lg(10a+9)+1]=lg(10a+10)
則由已知得,存在x∈(﹣∞,1],使不等式g(x)>lg(10a+10)成立,
而g(x)在(﹣∞,1]單增,
∴ ![]()
∴ ![]()
∴ ![]()
又 ![]()
又∵ ![]()
∴ ![]()
∴ ![]()
【解析】(1)由函數 ![]() 是奇函數,f(x)=lg(10x+1)+bx是偶函數,可得g(0)=0,f(﹣1)=f(1),進而可得a和b的值.(2)g(x)在(﹣∞,+∞)單調遞增,且g(x)為奇函數.若g(t2﹣2t)+g(2t2﹣k)>0恒成立,則3t2﹣2t>k,t∈[0,+∞)恒成立,令F(x)=3t2﹣2t,求其最值,可得答案;(3)h(x)=lg(10x+1),若存在x∈(﹣∞,1],使不等式g(x)>lg(10a+10)成立,則
是奇函數,f(x)=lg(10x+1)+bx是偶函數,可得g(0)=0,f(﹣1)=f(1),進而可得a和b的值.(2)g(x)在(﹣∞,+∞)單調遞增,且g(x)為奇函數.若g(t2﹣2t)+g(2t2﹣k)>0恒成立,則3t2﹣2t>k,t∈[0,+∞)恒成立,令F(x)=3t2﹣2t,求其最值,可得答案;(3)h(x)=lg(10x+1),若存在x∈(﹣∞,1],使不等式g(x)>lg(10a+10)成立,則 ![]() ,解得答案.
,解得答案.
【考點精析】解答此題的關鍵在于理解函數單調性的判斷方法的相關知識,掌握單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較,以及對函數奇偶性的性質的理解,了解在公共定義域內,偶函數的加減乘除仍為偶函數;奇函數的加減仍為奇函數;奇數個奇函數的乘除認為奇函數;偶數個奇函數的乘除為偶函數;一奇一偶的乘積是奇函數;復合函數的奇偶性:一個為偶就為偶,兩個為奇才為奇.


科目:高中數學 來源: 題型:
【題目】為了解今年某校高三畢業班準備報考飛行員學生的體重情況,將所得的數據整理后,畫出了頻率分布直方圖(如圖),已知圖中從左到右的前3個小組的頻率之比為1:2:3,其中第2小組的頻數為15.
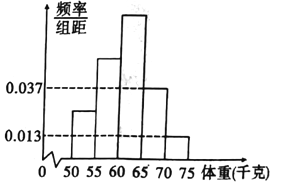
(1)求該校報考飛行員的總人數;
(2)以這所學校的樣本數據來估計全省的總體數據,若從全省報考飛行員的同學中(人數很多)任選三人,設![]() 表示體重超過65公斤的學生人數,求
表示體重超過65公斤的學生人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在區間
在區間![]() 上有最大值4和最小值1.設
上有最大值4和最小值1.設![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上有解,求實數
上有解,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() 有三個不同的實數解,求實數
有三個不同的實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠有一批貨物由海上從甲地運往乙地,已知輪船的最大航行速度為60海里/小時,甲地至乙地之間的海上航行距離為600海里,每小時的運輸成本由燃料費和其它費用組成,輪船每小時的燃料費與輪船速度的平方成正比,比例系數為0.5,其它費用為每小時1250元.
(1)請把全程運輸成本![]() (元)表示為速度
(元)表示為速度![]() (海里/小時)的函數,并指明定義域;
(海里/小時)的函數,并指明定義域;
(2)為使全程運輸成本最小,輪船應以多大速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)若函數![]() 在
在![]() 處的切線平行于直線
處的切線平行于直線![]() ,求實數a的值;
,求實數a的值;
(Ⅱ)判斷函數![]() 在區間
在區間![]() 上零點的個數;
上零點的個數;
(Ⅲ)在(Ⅰ)的條件下,若在![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com