
(Ⅰ)求![]() 的通項;
的通項;
(Ⅱ)求![]() 的前n項和
的前n項和![]() 。
。
(21)本小題主要考查等比數列的基本知識,考查分析問題能力和推理能力.
解:(I)由210S30-(210+1)S20+S10=0得
210(S30-S20)=S20-S10,
即 210(a21+a22+…+a30)=a11+a12+…+a20,
可得 210·q10(a11+a12+…+a20)=a11+a12+…+a20.
因為an>0,所以
210q10=1,
解得q=![]() ,因而
,因而
an=a1qn-1=![]() ,n=1,2,….
,n=1,2,….
(II)因為{an}是首項a1=![]() 、公比q=
、公比q=![]() 的等比數列,故
的等比數列,故
Sn= =1-
=1-![]() ,nSn=n-
,nSn=n-![]() .
.
則數列{nSn}的前n項和
Tn=(1+2+…+n)-(![]() +
+![]() +…+
+…+![]() ),
),
![]() (1+2+…+n)-(
(1+2+…+n)-(![]() +
+![]() +…+
+…+![]() ).
).
前兩式相減,得
![]() (1+2+…+n)-(
(1+2+…+n)-(![]() +
+![]() +…+
+…+![]() )+
)+![]()
=![]() -
-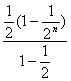 +
+![]() ,
,
即 Tn=![]()


國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com