設單調(diào)遞減數(shù)列
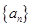
前

項和

,且

;
(1)求
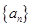
的通項公式;
(2)若
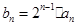
,求

前

項和

.
(1)
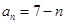
(2)
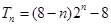
試題分析:當
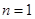
時,
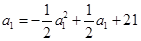
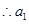
=6(

舍去) 1’
當
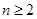
時,
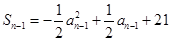
① 2’

②
②
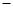
①得:
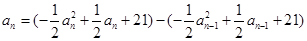
3’
整理的:
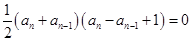
4’
故
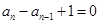
(

=0與數(shù)列遞減矛盾舍去)
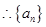
是公差為
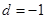
的等差數(shù)列 5’
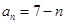
6’
(2)
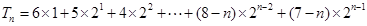
③ 7’
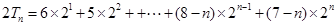
④ 8’
④
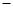
③:
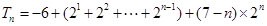
10’
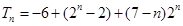
11’
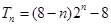
12’
點評:第一問中數(shù)列由前n項和求通項用到了
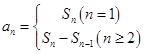
,第二問數(shù)列求和采用了錯位相減法,此法適用于通項為關于n的一次式與指數(shù)式的乘積形式的數(shù)列
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
設數(shù)列

的前

項和為

,

,

.
(Ⅰ)求數(shù)列

的通項公式;
(Ⅱ)設

是數(shù)列

的前
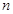
項和,求

.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
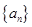
是公比為正數(shù)的等比數(shù)列,
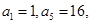
則數(shù)列
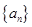
的前9項和
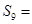
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知各項均為正數(shù)的等比數(shù)列{

},

,則

的值為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
首項為1,公比為2的等比數(shù)列的前5項和

=________.
查看答案和解析>>

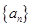 前
前 項和
項和 ,且
,且 ;
;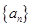 的通項公式;
的通項公式;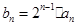 ,求
,求 前
前 項和
項和 .
. 新思維小冠軍100分作業(yè)本系列答案
新思維小冠軍100分作業(yè)本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案