
已知數列 的前
的前 項和為
項和為 ,且滿足
,且滿足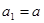 (
(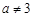 ),
),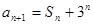 ,設
,設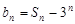 ,
,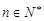 .
.
(1)求證:數列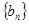 是等比數列;
是等比數列;
(2)若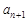 ≥
≥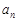 ,
,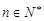 ,求實數
,求實數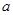 的最小值;
的最小值;
(3)當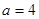 時,給出一個新數列
時,給出一個新數列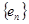 ,其中
,其中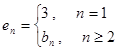 ,設這個新數列的前
,設這個新數列的前 項和為
項和為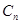 ,若
,若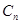 可以寫成
可以寫成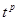 (
(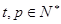 且
且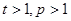 )的形式,則稱
)的形式,則稱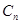 為“指數型和”.問
為“指數型和”.問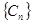 中的項是否存在“指數型和”,若存在,求出所有“指數型和”;若不存在,請說明理由.
中的項是否存在“指數型和”,若存在,求出所有“指數型和”;若不存在,請說明理由.
(1)根據等比數列的定義,相鄰兩項的比值為定值。
(2)-9
(3)①當 為偶數時,
為偶數時,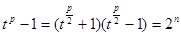 ,存在正整 數
,存在正整 數 ,使得
,使得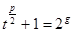 ,
,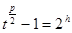 ,
,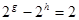 ,
, ,所以
,所以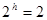 且
且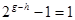
 ,
,
相應的 ,即有
,即有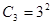 ,
, 為“指數型和”;
為“指數型和”;
②當 為奇數時,
為奇數時, ,由于
,由于 是
是 個奇數之和,仍為奇數,又
個奇數之和,仍為奇數,又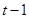 為正偶數,所以
為正偶數,所以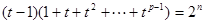 不成立,此時沒有“指數型和
不成立,此時沒有“指數型和
解析試題分析:解:(1)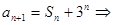
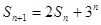 ,
,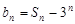 ,
,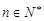 ,當
,當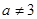 時,
時,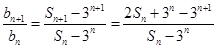 =2,所以
=2,所以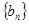 為等比數列.
為等比數列. 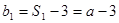 ,
, .
.
(2) 由(1)可得

 ;
; 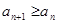 ,
,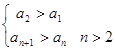 ,
,
所以 ,且
,且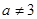 .所以
.所以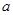 的最小值為-9
的最小值為-9
(3)由(1)當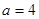 時 ,
時 ,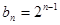
當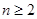 時,
時,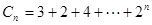
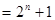 ,
,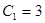 ,
,
所以對正整數 都有
都有 .
.
由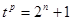 ,
, ,(
,(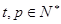 且
且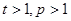 ),
),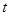 只能是不小于3的奇數.
只能是不小于3的奇數.
①當 為偶數時,
為偶數時,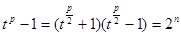 ,
,
因為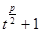 和
和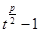 都是大于1的正整數,
都是大于1的正整數,
所以存在正整 數 ,使得
,使得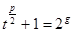 ,
,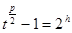 ,
,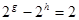 ,
, ,所以
,所以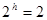 且
且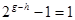
 ,
,
相應的 ,即有
,即有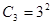 ,
, 為“指數型和”;
為“指數型和”;
②當 為奇數時,
為奇數時, ,由于
,由于 是
是 個奇數之和,
個奇數之和,
仍為奇數,又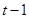 為正偶數,所以
為正偶數,所以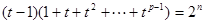 不成立,此時沒有“指數型和”
不成立,此時沒有“指數型和”
考點:數列和函數的 綜合運用
點評:解決的關鍵是能利用數列的定義和數列的單調性來求解參數的值,同事能借助于新定義來求解,屬于基礎題。


科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知數列 的各項排成如圖所示的三角形數陣,數陣中每一行的第一個數
的各項排成如圖所示的三角形數陣,數陣中每一行的第一個數 構成等差數列
構成等差數列 ,
, 是
是 的前n項和,且
的前n項和,且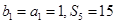

( I )若數陣中從第三行開始每行中的數按從左到右的順序均構成公比為正數的等比數列,且公比相等,已知 ,求
,求 的值;
的值;
(Ⅱ)設 ,求
,求 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com