
【題目】如圖所示,在直三棱柱ABC-A1B1C1中,CA=4,CB=4,CC1=2![]() ,∠ACB=90°,點M在線段A1B1上.
,∠ACB=90°,點M在線段A1B1上.

(1)若A1M=3MB1,求異面直線AM和A1C所成角的余弦值;
(2)若直線AM與平面ABC1所成角為30°,試確定點M的位置.
【答案】(1)![]() ;(2)線段A1B1的中點.
;(2)線段A1B1的中點.
【解析】
試題分析:本題考查用空間向量法解決立體幾何問題,最簡單的方法是建立空間直角坐標系,如以C為坐標原點,分別以CA,CB,CC1所在直線為x軸,y軸,z軸,建立如圖所示的空間直角坐標系,寫出各點坐標,(1)求得相應向量,異面直線AM和A1C所成角的余弦值就是cos〈![]() ,
,![]() 〉的絕對值;(2)先求得平面ABC1的法向量為n,因為點M在線段A1B1上,可設M(x,4-x,2
〉的絕對值;(2)先求得平面ABC1的法向量為n,因為點M在線段A1B1上,可設M(x,4-x,2![]() ),利用法向量n與向量
),利用法向量n與向量![]() 的夾角(銳角)與直線和平面所成的角互余可得,即由|cos〈n,
的夾角(銳角)與直線和平面所成的角互余可得,即由|cos〈n,![]() 〉|=
〉|=![]() 可求得
可求得![]() ,從而確定
,從而確定![]() 的位置.
的位置.
試題解析:方法一 (坐標法)
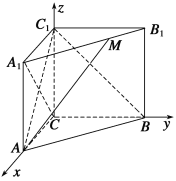
以C為坐標原點,分別以CA,CB,CC1所在直線為x軸,y軸,z軸,建立如圖所示的空間直角坐標系,則C(0,0,0),A(4,0,0),A1(4,0,2![]() ),B1(0,4,2
),B1(0,4,2![]() ).
).
(1)因為A1M=3MB1,所以M(1,3,2![]() ).
).
所以![]() =(4,0,2
=(4,0,2![]() ),
),![]() =(-3,3,2
=(-3,3,2![]() ).
).
所以cos〈![]() ,
,![]() 〉=
〉=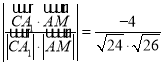 =-
=-![]() .
.
所以異面直線AM和A1C所成角的余弦值為![]() .
.
(2)由A(4,0,0),B(0,4,0),C1(0,0,2![]() ),
),
知![]() =(-4,4,0),
=(-4,4,0),![]() =(-4,0,2
=(-4,0,2![]() ).
).
設平面ABC1的法向量為n=(a,b,c),
由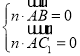 得
得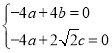
令a=1,則b=1,c=![]() ,
,
所以平面ABC1的一個法向量為n=(1,1,![]() ).
).
因為點M在線段A1B1上,所以可設M(x,4-x,2![]() ),
),
所以![]() =(x-4,4-x,2
=(x-4,4-x,2![]() ).
).
因為直線AM與平面ABC1所成角為30°,
所以|cos〈n,![]() 〉|=sin 30°=
〉|=sin 30°=![]() .
.
由|n![]()
![]() |=|n||
|=|n||![]() ||cos〈n,
||cos〈n,![]() 〉|,得
〉|,得
|1![]() (x-4)+1
(x-4)+1![]() (4-x)+
(4-x)+![]()
![]() 2
2![]() |
|
=2![]()
![]()
![]()
![]() ,
,
解得x=2或x=6.
因為點M在線段A1B1上,所以x=2,
即點M(2,2,2![]() )是線段A1B1的中點.
)是線段A1B1的中點.
方法二 (選基底法)
由題意得CC1⊥CA,CA⊥CB,CC1⊥CB,取![]() ,
,![]() ,
,![]() 作為一組基底,
作為一組基底,
則有|![]() |=|
|=|![]() |=4,|
|=4,|![]() |=2
|=2![]() ,
,
且![]()
![]()
![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]() =0.
=0.
(1)由![]() =3
=3![]() ,則
,則![]() =
=![]()
![]() =
=![]()
![]() =
=![]()
![]() -
-![]()
![]() ,
,
∴![]() =
=![]() +
+![]() =
=![]() +
+![]()
![]() -
-![]()
![]() ,
,
且|![]() |=
|=![]()
![]() =-
=-![]() -
-![]() ,且|
,且|![]() |=2
|=2![]() ,
,
∴![]()
![]() =4
=4
∴cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]() .
.
即異面直線AM與A1C所成角的余弦值為![]() .
.
(2)設A1M=λA1B1,則![]() =
=![]() +λ
+λ![]() -λ
-λ![]() .
.
又![]() =
=![]() -
-![]() ,
,![]() =
=![]() -
-![]() ,
,
設面ABC1的法向量為n=x![]() +y
+y![]() +z
+z![]() ,
,
則![]()
![]() =8z-16x=0,
=8z-16x=0,![]()
![]() =16y-16x=0,
=16y-16x=0,
不妨取x=y=1,z=2,
則n=![]() +
+![]() +2
+2![]() 且|n|=8,
且|n|=8,
|![]() |=
|=![]() ,
,![]() =16,
=16,
又AM與面ABC1所成的角為30°,則應有
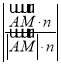 =
=![]() =
=![]() ,
,
得λ=![]() ,即M為A1B1的中點.
,即M為A1B1的中點.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】經市場調查,某門市部的一種小商品在過去的20天內的日銷售量(件)與價格(元)均為時間![]() (天)的函數,且日銷售量近似滿足函數
(天)的函數,且日銷售量近似滿足函數![]() (件),而且銷售價格近似滿足于
(件),而且銷售價格近似滿足于 (元).
(元).
(1)試寫出該種商品的日銷售額![]() 與時間
與時間![]() 的函數表達式;
的函數表達式;
(2)求該種商品的日銷售額![]() 的最大值與最小值.
的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是圓
是圓![]() 內一個定點,
內一個定點,![]() 是圓上任意一點.線段
是圓上任意一點.線段![]() 的垂直平分線和半徑
的垂直平分線和半徑![]() 相交于點
相交于點![]() .
.
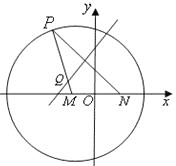
(Ⅰ)當點![]() 在圓上運動時,點
在圓上運動時,點![]() 的軌跡
的軌跡![]() 是什么曲線?并求出其軌跡方程;
是什么曲線?并求出其軌跡方程;
(Ⅱ)過點![]() 作直線
作直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 關于原點
關于原點![]() 的對稱點為
的對稱點為![]() ,求
,求![]() 的面積
的面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P—ABCD的底面ABCD是正方形,側棱PD⊥底面ABCD,PD=DC,E是PC的中點.

(Ⅰ)證明PA//平面BDE;
(Ⅱ)求二面角B—DE—C的平面角的余弦值;
(Ⅲ)在棱PB上是否存在點F,使PB⊥平面DEF?證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com