
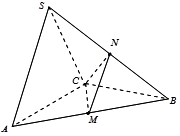
在三棱錐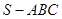 中,
中, 是邊長為
是邊長為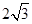 的正三角形,平面
的正三角形,平面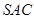 ⊥平面
⊥平面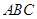 ,
,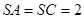 ,
,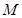 、
、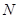 分別為
分別為 、
、 的中點.
的中點.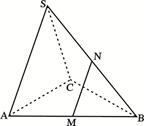
(Ⅰ)證明: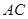 ⊥
⊥ ;
;
(Ⅱ)求三棱錐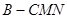 的體積.
的體積.
(Ⅰ)詳見解析;(Ⅱ)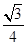 .
.
解析試題分析:(Ⅰ)證明: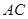 ⊥
⊥ ,證明兩線垂直,只需證明一線垂直另一線所在的平面,從圖上看現有的平面都不滿足,需重新構造,注意到
,證明兩線垂直,只需證明一線垂直另一線所在的平面,從圖上看現有的平面都不滿足,需重新構造,注意到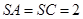 ,
, 是邊長為
是邊長為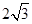 的正三角形,可考慮取
的正三角形,可考慮取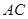 中點
中點 ,連結
,連結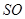 ,
, ,這樣易證
,這樣易證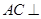 平面
平面 ,從而可得
,從而可得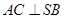 ;(Ⅱ)求三棱錐
;(Ⅱ)求三棱錐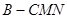 的體積,在這里
的體積,在這里 的面積不容易求,且B到平面
的面積不容易求,且B到平面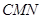 的距離也不易求,故可等體積轉化,換為求三棱錐
的距離也不易求,故可等體積轉化,換為求三棱錐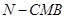 的體積,由題意,
的體積,由題意,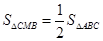 ,
,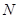 為
為 的中點,故
的中點,故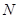 到平面
到平面 的距離就等于點
的距離就等于點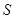 到平面
到平面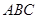 的距離的
的距離的 ,從而可得三棱錐
,從而可得三棱錐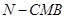 的體積.
的體積.
試題解析:(Ⅰ)證明:如圖,取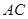 中點
中點 ,連結
,連結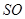 ,
, .
.
∵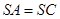 ,∴
,∴ 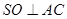 . 2分
. 2分
又∵ 是正三角形, ∴
是正三角形, ∴ .
.
∵  ,
,
∴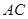 ⊥平面
⊥平面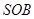 . 4分
. 4分
又 在平面
在平面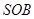 內,∴
內,∴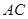 ⊥
⊥ . 6分
. 6分
(Ⅱ)∵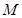 是
是 的中點,
的中點,
∴ . 8分
. 8分
∵平面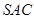 ⊥平面
⊥平面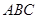 ,
,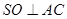 ,∴
,∴ 平面
平面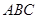 .
.
又∵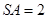 ,
,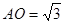 ,∴
,∴ ,即點
,即點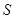 到平面
到平面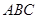 的距離為1.
的距離為1.
∵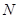 是
是 的中點,∴點
的中點,∴點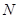 到平面
到平面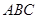 的距離為
的距離為 . 10分
. 10分
∴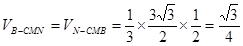 . 12分
. 12分
考點:線面垂直,幾何體的體積.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:解答題
如圖,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
(1)求證:AC⊥BB1;
(2)若P是棱B1C1的中點,求平面PAB將三棱柱分成的兩部分體積之比.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com