
 的函數
的函數 ,其導函數為
,其導函數為 .記函數
.記函數 在區間
在區間 上的最大值為
上的最大值為 .
. 在
在 處有極值
處有極值 ,試確定
,試確定 的值;
的值; ,證明對任意的
,證明對任意的 ,都有
,都有 ;
; 對任意的
對任意的 恒成立,試求
恒成立,試求 的最大值.
的最大值. ,
, ;(2)證明詳見解析;(3)
;(2)證明詳見解析;(3) .
. 求導,由于
求導,由于 在x=1處有極值
在x=1處有極值 ,則
,則 ,
, ,列出方程組,解出b和c的值,由于得到了兩組值,則需要驗證看是否符合已知條件,若不符合需舍掉;第二問,可以利用二次函數圖象和性質直接證明
,列出方程組,解出b和c的值,由于得到了兩組值,則需要驗證看是否符合已知條件,若不符合需舍掉;第二問,可以利用二次函數圖象和性質直接證明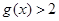 ,也可以利用反證法證明出矛盾,從而得到正確結論;第三問,結合第二問的結論,可以直接得到
,也可以利用反證法證明出矛盾,從而得到正確結論;第三問,結合第二問的結論,可以直接得到 時的情況,當
時的情況,當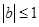 時需分
時需分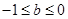 ,
, ,
, 三種情況討論,最后綜合所有情況再得出結論.
三種情況討論,最后綜合所有情況再得出結論. ,由
,由 在
在 處有極值
處有極值 ,可得
,可得 ,解得,
,解得, 或
或 2分
2分 ,
, ,則
,則 ,此時函數
,此時函數 沒有極值; 3分
沒有極值; 3分 ,
, ,則
,則 ,此時當
,此時當 變化時,
變化時, ,
, 的變化情況如下表:
的變化情況如下表: | 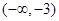 | 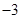 | 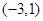 |  | 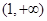 |
 | 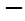 |  |  |  |  |
 | ↘ | 極小值 | ↗ | 極大值 | ↘ |
 時,
時, 有極大值
有極大值 ,故
,故 ,
, 即為所求。 4分
即為所求。 4分
 時,函數
時,函數 的對稱軸
的對稱軸 位于區間
位于區間 之外
之外 在區間
在區間 上的最值在兩端點處取得,故
上的最值在兩端點處取得,故 應是
應是 和
和 中較大的一個
中較大的一個

 ,即
,即 8分
8分 ,所以函數
,所以函數 的對稱軸
的對稱軸 位于區間
位于區間 之外,
之外, 在區間
在區間 上的最值在兩端點處取得,故
上的最值在兩端點處取得,故 應是
應是 和
和 中較大的一個,
中較大的一個,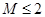 ,則
,則 ,將上述兩式相加得: 6分
,將上述兩式相加得: 6分 ,得
,得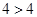 ,產生矛盾,
,產生矛盾, 8分
8分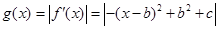
 時,由(2)可知
時,由(2)可知 ; 9分
; 9分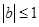 時,函數
時,函數 的對稱軸
的對稱軸 位于區間
位于區間 之內,
之內, ,由
,由 ,有
,有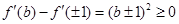
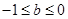 ,則
,則 ,則
,則 ,
,
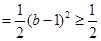 11分
11分 ,則
,則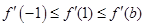 ,則
,則

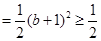 13分
13分 、
、 都有
都有
 ,
, 時,
時,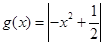 在區間
在區間 上的最大值
上的最大值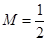 ,故
,故 對任意的
對任意的 、
、 恒成立的
恒成立的 的最大值為
的最大值為 。 14分
。 14分

 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源:不詳 題型:解答題
 ,其中a,b∈R
,其中a,b∈R 成立,試用a表示出b的取值范圍.
成立,試用a表示出b的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.f(x)=g(x) | B.f(x)-g(x)為常數 |
| C.f(x)=g(x)=0 | D.f(x)+g(x)為常數 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 1 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com