圖形P－ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA＝AB，Q是PC中點．AC，BD交于O點．
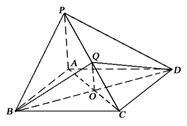
（1）二面角Q－BD－C的大小：
（2）求二面角B－QD－C的大小．
（1）
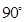（2）
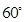
【解析】
試題分析：連QO，則QO∥PA且QO＝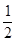
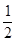PA＝AB
∵ PA⊥面ABCD
∴ QO⊥面ABCD
面QBD過QO，
∴ 面QBD⊥面ABCD
故二面角Q－BD－C等于90°．
（Ⅱ）解：過O作OH⊥QD，垂足為H，連CH．
∵ 面QBD⊥面BCD，
又∵ CO⊥BD
CO⊥面QBD
CH在面QBD內的射影是OH
∵ OH⊥QD
∴ CH⊥QD
于是∠OHC是二面角的平面角．
設正方形ABCD邊長2，
則OQ＝1，O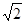D＝
，QD＝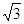
．
∵ OH·QD＝OQ·OD
∴ OH＝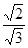
．
又OC＝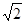
在Rt△COH中：tan∠OHC＝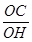
＝·＝
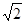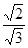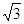
∴ ∠OHC＝60°
故二面角B－QD－C等于60°．
考點：二面角求解
點評：本題還可用空間向量的方法求二面角
暑假作業海燕出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案
第三學期贏在暑假系列答案科目：高中數學 來源：湖北省荊州中學2008高考復習立體幾何基礎題題庫一(有詳細答案)人教版 人教版 題型：044
在立體圖形
P－ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA＝AB，Q是PC中點．AC，BD交于O點．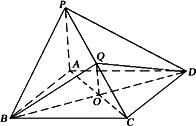
(Ⅰ)求二面角Q－BD－C的大小：
(Ⅱ)求二面角B－QD－C的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
在立體圖形P－ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA＝AB，Q是PC中點．
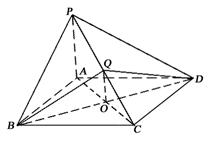AC，BD交于O點．
（Ⅰ）求二面角Q－BD－C的大小：
（Ⅱ）求二面角B－QD－C的大小．
查看答案和解析>>
科目：高中數學 來源：2014屆江西省高二第二次月考理科數學試卷（解析版） 題型：解答題
圖形P－ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA＝AB，Q是PC中點．AC，BD交于O點．
（1）二面角Q－BD－C的大小：
（2求二面角B－QD－C的大小．
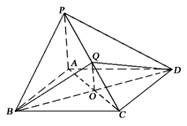
查看答案和解析>>
科目：高中數學 來源：2010-2011學年云南省高二上學期第一次月考文科數學卷 題型：解答題
（本題滿分12分）
在立體圖形P－ABCD中，底面ABCD是一個直角梯形，∠BAD＝90°，AD∥BC，
AB＝BC＝a，AD=PA＝2a，E是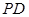
邊的中點，且PA⊥底面ABCD。
（1）求證：BE⊥PD
（2）求證：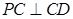
（3）求異面直線AE與CD所成的角．
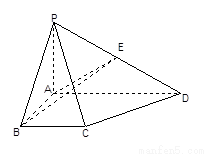
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com