
【題目】已知橢圓C:![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,且過(guò)點(diǎn)(1,
,且過(guò)點(diǎn)(1,![]() ).
).
(1)求橢圓C的方程;
(2)設(shè)與圓O:x2+y2=![]() 相切的直線l交橢圓C于A,B兩點(diǎn),求△OAB面積的最大值,及取得最大值時(shí)直線l的方程.
相切的直線l交橢圓C于A,B兩點(diǎn),求△OAB面積的最大值,及取得最大值時(shí)直線l的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)利用離心率把橢圓方程設(shè)成:![]() ,代入橢圓上的點(diǎn)可得橢圓方程.
,代入橢圓上的點(diǎn)可得橢圓方程.
(2)設(shè)直線為![]() ,
,![]() ,聯(lián)立直線方程和橢圓方程并消元得到
,聯(lián)立直線方程和橢圓方程并消元得到![]() ,利用韋達(dá)定理把面積表示關(guān)于
,利用韋達(dá)定理把面積表示關(guān)于![]() 的函數(shù),利用基本不等式求面積的最大值,注意討論直線的斜率不存在情形.
的函數(shù),利用基本不等式求面積的最大值,注意討論直線的斜率不存在情形.
(1)由題意可得,![]() ,故
,故![]() ,
,![]() ,
,
所以橢圓方程為![]() .
.
將點(diǎn)![]() 代入橢圓方程,可得
代入橢圓方程,可得![]() ,故
,故![]() ,
,
即有橢圓的方程為![]() .
.
(2)①當(dāng)![]() 不存在時(shí),
不存在時(shí),![]() 時(shí),可得
時(shí),可得![]() ,
,
![]() ;
;
②當(dāng)![]() 存在時(shí),設(shè)直線為
存在時(shí),設(shè)直線為![]() ,
,![]() ,
,
將直線![]() 代入橢圓方程可得
代入橢圓方程可得![]() ,
,
![]() ,
,![]() ,
,
由直線![]() 與圓
與圓![]() 相切,可得
相切,可得![]() ,
,
即有![]() ,
,
又![]()
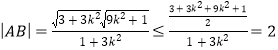 ,
,
當(dāng)且僅當(dāng)![]() 9即
9即![]() 時(shí)等號(hào)成立,
時(shí)等號(hào)成立,
此時(shí)![]() ,
,
即![]() 有面積的最大值為
有面積的最大值為![]() ,此時(shí)直線方程
,此時(shí)直線方程![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校倡導(dǎo)為特困學(xué)生募捐,要求在自動(dòng)購(gòu)水機(jī)處每購(gòu)買一瓶礦泉水,便自覺(jué)向捐款箱中至少投入一元錢.現(xiàn)統(tǒng)計(jì)了連續(xù)5天的售出礦泉水箱數(shù)和收入情況,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
學(xué)校計(jì)劃將捐款以獎(jiǎng)學(xué)金的形式獎(jiǎng)勵(lì)給品學(xué)兼優(yōu)的特困生,規(guī)定:特困生綜合考核前20名,獲一等獎(jiǎng)學(xué)金500元;綜合考核21-50名,獲二等獎(jiǎng)學(xué)金300元;綜合考核50名以后的不獲得獎(jiǎng)學(xué)金.
(1)若![]() 與
與![]() 成線性相關(guān),則某天售出9箱水時(shí),預(yù)計(jì)收入為多少元?
成線性相關(guān),則某天售出9箱水時(shí),預(yù)計(jì)收入為多少元?
(2)甲乙兩名學(xué)生獲一等獎(jiǎng)學(xué)金的概率均為![]() ,獲二等獎(jiǎng)學(xué)金的概率均為
,獲二等獎(jiǎng)學(xué)金的概率均為![]() ,不獲得獎(jiǎng)學(xué)金的概率均為
,不獲得獎(jiǎng)學(xué)金的概率均為![]() ,已知甲乙兩名學(xué)生獲得哪個(gè)等級(jí)的獎(jiǎng)學(xué)金相互獨(dú)立,求甲乙兩名學(xué)生所獲得獎(jiǎng)學(xué)金之和
,已知甲乙兩名學(xué)生獲得哪個(gè)等級(jí)的獎(jiǎng)學(xué)金相互獨(dú)立,求甲乙兩名學(xué)生所獲得獎(jiǎng)學(xué)金之和![]() 的分布列及數(shù)學(xué)期望;
的分布列及數(shù)學(xué)期望;
附:回歸方程![]() ,其中
,其中 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 的圖象是由函數(shù)
的圖象是由函數(shù)![]() 的圖象經(jīng)如下變換得到:先將
的圖象經(jīng)如下變換得到:先將![]() 圖象上所有點(diǎn)的縱坐標(biāo)伸長(zhǎng)到原來(lái)的
圖象上所有點(diǎn)的縱坐標(biāo)伸長(zhǎng)到原來(lái)的![]() 倍(橫坐標(biāo)不變),再將所得到的圖象向右平移
倍(橫坐標(biāo)不變),再將所得到的圖象向右平移![]() 個(gè)單位長(zhǎng)度.
個(gè)單位長(zhǎng)度.
(1)求函數(shù)![]() 的解析式,并求其圖象的對(duì)稱軸方程;
的解析式,并求其圖象的對(duì)稱軸方程;
(2)已知關(guān)于![]() 的方程
的方程![]() 在
在![]() 內(nèi)有兩個(gè)不同的解
內(nèi)有兩個(gè)不同的解![]() 、
、![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]()
![]() .
.
(Ⅰ)求函數(shù)![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(Ⅱ)在銳角![]() 中,若
中,若![]() ,且能蓋住
,且能蓋住![]() 的最小圓的面積為
的最小圓的面積為![]() ,求
,求![]() 周長(zhǎng)的取值范圍.
周長(zhǎng)的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】![]() 是空氣質(zhì)量的一個(gè)重要指標(biāo),我國(guó)
是空氣質(zhì)量的一個(gè)重要指標(biāo),我國(guó)![]() 標(biāo)準(zhǔn)采用世衛(wèi)組織設(shè)定的最寬限值,即
標(biāo)準(zhǔn)采用世衛(wèi)組織設(shè)定的最寬限值,即![]() 日均值在
日均值在![]() 以下空氣質(zhì)量為一級(jí),在
以下空氣質(zhì)量為一級(jí),在![]() 之間空氣質(zhì)量為二級(jí),在
之間空氣質(zhì)量為二級(jí),在![]() 以上空氣質(zhì)量為超標(biāo).如圖是某地
以上空氣質(zhì)量為超標(biāo).如圖是某地![]() 月
月![]() 日到
日到![]() 日
日![]() 日均值(單位:
日均值(單位:![]() )的統(tǒng)計(jì)數(shù)據(jù),則下列敘述不正確的是( )
)的統(tǒng)計(jì)數(shù)據(jù),則下列敘述不正確的是( )
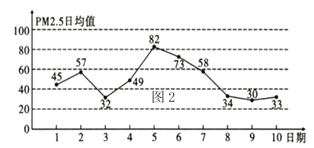
A.從![]() 日到
日到![]() 日,
日,![]() 日均值逐漸降低
日均值逐漸降低
B.這![]() 天的
天的![]() 日均值的中位數(shù)是
日均值的中位數(shù)是![]()
C.這![]() 天中
天中![]() 日均值的平均數(shù)是
日均值的平均數(shù)是![]()
D.從這![]() 天的日均
天的日均![]() 監(jiān)測(cè)數(shù)據(jù)中隨機(jī)抽出一天的數(shù)據(jù),空氣質(zhì)量為一級(jí)的概率是
監(jiān)測(cè)數(shù)據(jù)中隨機(jī)抽出一天的數(shù)據(jù),空氣質(zhì)量為一級(jí)的概率是![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖(示意),公路AM、AN圍成的是一塊頂角為鈍角α的角形耕地,其中![]() .在該塊土地中
.在該塊土地中![]() 處有一小型建筑,經(jīng)測(cè)量,它到公路
處有一小型建筑,經(jīng)測(cè)量,它到公路![]() 、
、![]() 的距離
的距離![]() 、
、![]() 分別為
分別為![]() ,
,![]() .現(xiàn)要過(guò)點(diǎn)
.現(xiàn)要過(guò)點(diǎn)![]() 修建一條直線公路
修建一條直線公路![]() ,將三條公路圍成的區(qū)域
,將三條公路圍成的區(qū)域![]() 建成一個(gè)工業(yè)園.設(shè)
建成一個(gè)工業(yè)園.設(shè)![]() ,
,![]()
![]() ,其中
,其中![]() .
.

(1)試建立![]() 間的等量關(guān)系;
間的等量關(guān)系;
(2)為盡量減少耕地占用,問(wèn)如何確定B點(diǎn)的位置,使得該工業(yè)園區(qū)的面積最小?并求最小面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2017年被稱為“新高考元年”,隨著上海、浙江兩地順利實(shí)施“語(yǔ)數(shù)外+3”新高考方案,新一輪的高考改革還將繼續(xù)在全國(guó)推進(jìn).遼寧地區(qū)也將于2020年開(kāi)啟新高考模式,今年秋季入學(xué)的高一新生將面臨從物理、化學(xué)、生物、政治、歷史、地理等6科中任選三科(共20種選法)作為自己將來(lái)高考“語(yǔ)數(shù)外+3”新高考方案中的“3”.某地區(qū)為了順利迎接新高考改革,在某學(xué)校理科班的200名學(xué)生中進(jìn)行了“學(xué)生模擬選科數(shù)據(jù)”調(diào)查,每個(gè)學(xué)生只能從表格中的20種課程組合選擇一種學(xué)習(xí).模擬選課數(shù)據(jù)統(tǒng)計(jì)如下表:
序號(hào) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
組合學(xué)科 | 物化生 | 物化政 | 物化歷 | 物化地 | 物生政 | 物生歷 | 物生地 |
人數(shù) | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序號(hào) | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
組合學(xué)科 | 物政歷 | 物政地 | 物歷地 | 化生政 | 化生歷 | 化生地 | 化政歷 |
人數(shù) | 5人 | 0人 | 5人 | …… | 40人 | …… | …… |
序號(hào) | 15 | 16 | 17 | 18 | 19 | 20 | |
組合學(xué)科 | 化政地 | 化歷地 | 生政歷 | 生政地 | 生歷地 | 政歷地 | 總計(jì) |
人數(shù) | …… | …… | …… | …… | …… | …… | 200人 |
為了解學(xué)生成績(jī)與學(xué)生模擬選課之間的關(guān)系,用分層抽樣的方法從這200名學(xué)生中抽取40人的樣本進(jìn)行分析。
(1)樣本中選擇組合6號(hào)“物生歷”的有多少人?樣本中同時(shí)選擇學(xué)習(xí)物理和歷史的有多少人?
(2)從樣本選擇學(xué)習(xí)物理且學(xué)習(xí)歷史的學(xué)生中隨機(jī)抽取3人,求這3人中至少有2人還要學(xué)習(xí)生物的概率。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】將給定的一個(gè)數(shù)列![]() :
:![]() ,
,![]() ,
,![]() ,…按照一定的規(guī)則依順序用括號(hào)將它分組,則可以得到以組為單位的序列.如在上述數(shù)列中,我們將
,…按照一定的規(guī)則依順序用括號(hào)將它分組,則可以得到以組為單位的序列.如在上述數(shù)列中,我們將![]() 作為第一組,將
作為第一組,將![]() ,
,![]() 作為第二組,將
作為第二組,將![]() ,
,![]() ,
,![]() 作為第三組,…,依次類推,第
作為第三組,…,依次類推,第![]() 組有
組有![]() 個(gè)元素(
個(gè)元素(![]() ),即可得到以組為單位的序列:
),即可得到以組為單位的序列:![]() ,
,![]() ,
,![]() ,…,我們通常稱此數(shù)列為分群數(shù)列.其中第1個(gè)括號(hào)稱為第1群,第2個(gè)括號(hào)稱為第2群,第3個(gè)數(shù)列稱為第3群,…,第
,…,我們通常稱此數(shù)列為分群數(shù)列.其中第1個(gè)括號(hào)稱為第1群,第2個(gè)括號(hào)稱為第2群,第3個(gè)數(shù)列稱為第3群,…,第![]() 個(gè)括號(hào)稱為第
個(gè)括號(hào)稱為第![]() 群,從而數(shù)列
群,從而數(shù)列![]() 稱為這個(gè)分群數(shù)列的原數(shù)列.如果某一個(gè)元素在分群數(shù)列的第
稱為這個(gè)分群數(shù)列的原數(shù)列.如果某一個(gè)元素在分群數(shù)列的第![]() 個(gè)群眾,且從第
個(gè)群眾,且從第![]() 個(gè)括號(hào)的左端起是第
個(gè)括號(hào)的左端起是第![]() 個(gè),則稱這個(gè)元素為第
個(gè),則稱這個(gè)元素為第![]() 群眾的第
群眾的第![]() 個(gè)元素.已知數(shù)列1,1,3,1,3,9,1,3,9,27,…,將數(shù)列分群,其中,第1群為(1),第2群為(1,3),第3群為(1,3,
個(gè)元素.已知數(shù)列1,1,3,1,3,9,1,3,9,27,…,將數(shù)列分群,其中,第1群為(1),第2群為(1,3),第3群為(1,3,![]() ),…,以此類推.設(shè)該數(shù)列前
),…,以此類推.設(shè)該數(shù)列前![]() 項(xiàng)和
項(xiàng)和![]() ,若使得
,若使得![]() 成立的最小
成立的最小![]() 位于第
位于第![]() 個(gè)群,則
個(gè)群,則![]() ( )
( )
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四棱錐![]() 的底面
的底面![]() 是菱形,
是菱形,![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() 底面
底面![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 中點(diǎn),
中點(diǎn),![]() .
.

(1)求直線![]() 與
與![]() 所成角的正弦值;
所成角的正弦值;
(2)求平面![]() 與平面
與平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com