
已知向量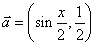 ,
,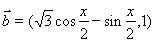 ,函數
,函數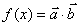 ,
,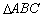 三個內角
三個內角 的對邊分別為
的對邊分別為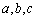 .
.
(1)求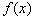 的單調遞增區間;
的單調遞增區間;
(2)若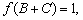
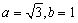 ,求
,求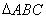 的面積
的面積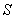 .
.
(1)函數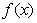 的單調增區間為
的單調增區間為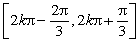
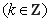 .
.
(2)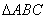 的面積
的面積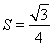 .
.
【解析】
試題分析:(1)根據平面向量的數量積,應用和差倍半的三角函數公式,將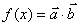 化簡為
化簡為
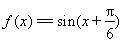 ,討論函數的單調性;
,討論函數的單調性;
(2) 本題解答可有兩種思路,在利用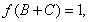 得到
得到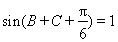 ,
,
求得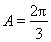 后,一是可應用正弦定理
后,一是可應用正弦定理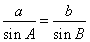 ,得到
,得到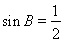 ,
,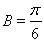 或者
或者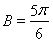 根據
根據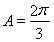 為鈍角,確定
為鈍角,確定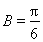 ,得
,得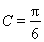 ;二是應用余弦定理,
;二是應用余弦定理, ,得
,得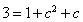 ,
,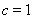 或
或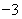 (舍去),進一步確定
(舍去),進一步確定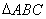 的面積
的面積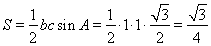 .
.
試題解析:(1)由題意得
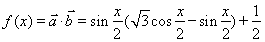
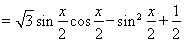
=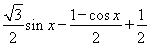 =
=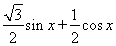
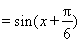 , 3分
, 3分
令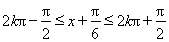

解得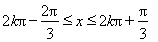
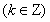
所以函數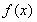 的單調增區間為
的單調增區間為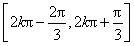
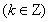 . 6分
. 6分
(2) 解法一:因為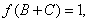 所以
所以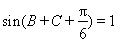 ,
,
又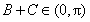 ,
,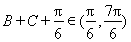 ,
,
所以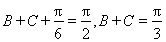 ,所以
,所以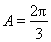 , 8分
, 8分
由正弦定理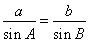 把
把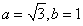 代入,得到
代入,得到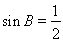 10分
10分
得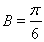 或者
或者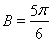 ,因為
,因為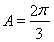 為鈍角,所以
為鈍角,所以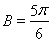 舍去
舍去
所以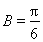 ,得
,得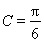 .
.
所以,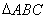 的面積
的面積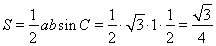 . 12分
. 12分
解法二:同上(略)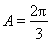 , 8分
, 8分
由余弦定理,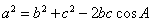 ,得
,得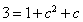 ,
,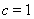 或
或 (舍去)10分
(舍去)10分
所以, 的面積
的面積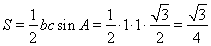 . 12分
. 12分
考點:平面向量的數量積,和差倍半的三角函數,正弦定理、余弦定理的應用,三角形面積公式.


科目:高中數學 來源:2011屆廣東省實驗中學、華師附中、深圳中學、廣雅中學高三上學期期末數學文卷 題型:解答題
(本小題滿分12分)
已知向量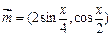 ,
, ,函數
,函數
(1)求 的最小正周期;
的最小正周期;
(2)若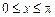 ,求
,求 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年安徽省六校教育研究會高三2月聯考理科數學試卷(解析版) 題型:解答題
已知向量 ,
, ,函數
,函數
(Ⅰ)求 的最大值;
的最大值;
(Ⅱ)在 中,設角
中,設角 ,
, 的對邊分別為
的對邊分別為 ,若
,若 ,且
,且 ?,求角
?,求角 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省廣州市育才中學高三(上)10月月考數學試卷(文科)(解析版) 題型:解答題
 ,
, ,函數
,函數 .
.查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省五校高三下學期第二次聯考理科數學試卷(解析版) 題型:解答題
已知向量 ,
, ,函數
,函數 .
.
(Ⅰ)若方程 在
在 上有解,求
上有解,求 的取值范圍;
的取值范圍;
(Ⅱ)在 中,
中, 分別是A,B,C所對的邊,當(Ⅰ)中的
分別是A,B,C所對的邊,當(Ⅰ)中的 取最大值且
取最大值且 時,求
時,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2010年南安一中高一下學期期末考試數學卷 題型:解答題
(本小題滿分12分)
已知向量 ,
, ,函數
,函數 .
.
(1)求函數 的最小正周期以及單調遞增區間;
的最小正周期以及單調遞增區間;
(2)若 時, 求
時, 求 的值域;
的值域;
(3)求方程 在
在 內的所有實數根之和.
內的所有實數根之和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com