
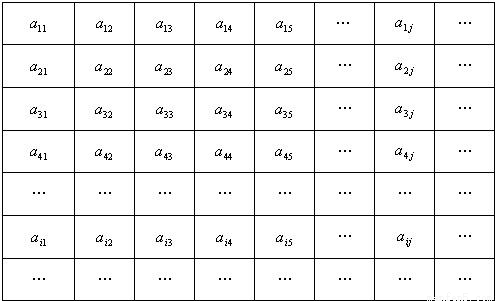
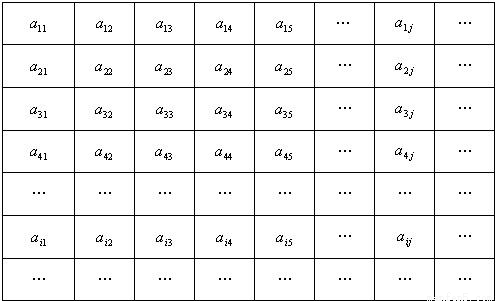
在下列由正數排成的數表中,每行上的數從左到右都成等比數列,并且所有公比都等于q,每列上的數從上到下都成等差數列.![]() 表示位于第
表示位于第![]() 行第
行第![]() 列的數,其中
列的數,其中![]() ,
,![]() ,
,![]() .
.
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
| … | … | … | … | … | … | … | … |
|
|
|
|
|
| … |
| … |
| … | … | … | … | … | … | … | … |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 求![]() 的計算公式;
的計算公式;
(Ⅲ)設數列{bn}滿足bn=ann,{bn}的前![]() 項和為
項和為![]() ,試比較
,試比較![]() 與Tn=
與Tn=![]() ( n∈N*) 的大小,并說明理由.
( n∈N*) 的大小,并說明理由.
解:(Ⅰ)設第4列公差為![]() ,則
,則 .
.
故![]() ,于是
,于是![]() .
.
由于![]() ,所以
,所以![]() ,故
,故![]() .
.
(Ⅱ)在第4列中,![]() .
.
由于第![]() 行成等比數列,且公比
行成等比數列,且公比![]() ,
,
所以, ![]() .
.
(Ⅲ)由(Ⅱ)可知![]() .即bn=
.即bn=![]() .
.
所以![]()
![]() .
.
即![]() ,
,
故![]() .
.
兩式相減,得![]()
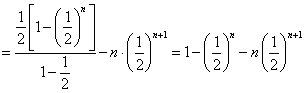 ,
,
所以![]() .
.
設f(x)=2-![]() -
-![]() ( x >0),
( x >0),
即f(x)=2-![]() -
-![]() =2-
=2-![]() =2-(2+ x)2-x.
=2-(2+ x)2-x.
因為f ′(x)= -[2-x+(2+ x)2-x(-1)ln2]= 2-x[(2+ x)ln2-1]
=2-x[ln22+ x - lne]=2-xln![]() ,
,
且當x>0時,x+2>2. 所以22+ x>22= 4.
于是![]() >
>![]() >1.
>1.
所以ln![]() >0.
>0.
又2-x>0,
所以在(0,+∞)上f ′(x) =2-xln![]() >0.
>0.
因此函數f(x)=2-![]() -
-![]() 在(0,+∞)單調遞增.
在(0,+∞)單調遞增.
所以![]() ( n∈N*)是遞增數列.
( n∈N*)是遞增數列.
同理設g(x)=![]() ( x >0),
( x >0),
因為g′(x)=![]() ?
?![]() = -
= -![]() <0 ( x >0),
<0 ( x >0),
故g(x)=![]() 在(0,+∞)單調遞減.
在(0,+∞)單調遞減.
所以Tn=![]() ( n∈N*)是遞減數列.
( n∈N*)是遞減數列.
容易計算S1=f(1)=![]() ,S2=f(2)=1,S3=f(3)=1
,S2=f(2)=1,S3=f(3)=1![]() ,S4=f(4)=1
,S4=f(4)=1![]() ,
,
T1= g(1)=1![]() ,T2= g(2)=1
,T2= g(2)=1![]() ,T3= g(3)=1
,T3= g(3)=1![]() ,T4= g(4)=1
,T4= g(4)=1![]() ,
,
顯然S1< T1,S2< T2,S3< T3,S4> T4,
所以當n≤3時,![]() <Tn;當n>3時,
<Tn;當n>3時,![]() >Tn.
>Tn.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| 1 |
| 8 |
| 5 |
| 16 |
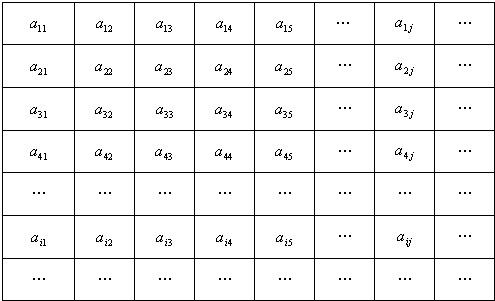
| 6n+11 |
| 5(n+1) |
查看答案和解析>>
科目:高中數學 來源: 題型:
在下列由正數排成的數表中,每行上的數從左到右都成等比數列,并且所有公比都等于![]() ,每列上的數從上到下都成等差數列.
,每列上的數從上到下都成等差數列.![]() 表示位于第
表示位于第![]() 行第
行第![]() 列的數,其中
列的數,其中![]() ,
,![]() ,
,![]() .
.
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
| … | … | … | … | … | … | … | … |
|
|
|
|
|
| … |
| … |
| … | … | … | … | … | … | … | … |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 求![]() 的計算公式;
的計算公式;
(Ⅲ)設數列{bn}滿足bn=ann,{bn}的前![]() 項和為
項和為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源:2007年北京市朝陽區高考數學二模試卷(文科)(解析版) 題型:解答題
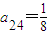 ,a42=1,
,a42=1,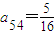 .
.
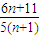 ( n∈N*)的大小,并說明理由.
( n∈N*)的大小,并說明理由.查看答案和解析>>
科目:高中數學 來源:2007年北京市朝陽區高考數學二模試卷(理科)(解析版) 題型:解答題
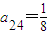 ,a42=1,
,a42=1,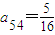 .
.
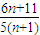 ( n∈N*)的大小,并說明理由.
( n∈N*)的大小,并說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com