【題目】手機支付也稱為移動支付
，是指允許移動用戶使用其移動終端（通常是手機）對所消費的商品或服務進行賬務支付的一種服務方式.繼卡類支付、網絡支付后，手機支付儼然成為新寵.某金融機構為了了解移動支付在大眾中的熟知度，對15-65歲的人群隨機抽樣調查，調查的問題是“你會使用移動支付嗎？”其中，回答“會”的共有100個人，把這100個人按照年齡分成5組，然后繪制成如圖所示的頻率分布表和頻率分布直方圖.
組數 | 第l組 | 第2組 | 第3組 | 第4組 | 第5組 |
分組 |
|
|
|
|
|
頻數 | 20 | 36 | 30 | 10 | 4 |
（1）求
；
（2）從第l，3，4組中用分層抽樣的方法抽取6人，求第l，3，4組抽取的人數：
（3）在（2）抽取的6人中再隨機抽取2人，求所抽取的2人來自同一個組的概率.
【答案】(1) 
；(2) 第1組2人,第3組3人，第4組1人；(3) 
【解析】
（1）直接計算
.
（2）根據分層抽樣的規律按照比例抽取.
（3）設第1組抽取的2人為
，
，第3組抽取的3人為
，
，
，第4組抽取的1人為
，排列出所有可能，再計算滿足條件的個數，相除得到答案.
解：（1）由題意可知，
，
（2）第1，3，4組共有60人，所以抽取的比例是
則從第1組抽取的人數為
,從第3組抽取的人數為
，從第4組抽取的人數為
；
（3）設第1組抽取的2人為，，第3組抽取的3人為，，，第4組抽取的1人為，則從這6人中隨機抽取2人有如下種情形：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
共有15個基本事件.
其中符合“抽取的2人來自同一個組”的基本事件有，，，共4個基本事件，
所以抽取的2人來自同一個組的概率.
科目：高中數學 來源： 題型：
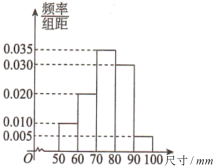
【題目】某工廠為檢驗車間一生產線工作是否正常，現從生產線中隨機抽取一批零件樣本，測量它們的尺寸(單位：
)并繪成頻率分布直方圖，如圖所示.根據長期生產經驗，可以認為這條生產線正常狀態下生產的零件尺寸
服從正態分布
，其中
近似為零件樣本平均數
，
近似為零件樣本方差
.
(1)求這批零件樣本的和的值（同一組中的數據用該組區間的中點值作代表）；
(2)假設生產狀態正常，求
；
(3)若從生產線中任取一零件，測量其尺寸為
，根據
原則判斷該生產線是否正常？
附：
；若
，則
， 
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在正方體
中，側面對角線
，
上分別有一點E，F，且
，則直線EF與平面ABCD所成的角的大小為（ ）
A.0°B.60°C.45°D.30°
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某書店剛剛上市了《中國古代數學史》，銷售前該書店擬定了5種單價進行試銷，每種單價（
元）試銷l天，得到如表單價（元）與銷量
（冊）數據：
單價 | 18 | 19 | 20 | 21 | 22 |
銷量 | 61 | 56 | 50 | 48 | 45 |
（l）根據表中數據，請建立關于的回歸直線方程：
（2）預計今后的銷售中，銷量（冊）與單價（元）服從（l）中的回歸方程，已知每冊書的成本是12元，書店為了獲得最大利潤，該冊書的單價應定為多少元？
附：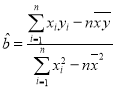
，
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2018年春季，世界各地相繼出現流感疫情，這已經成為全球性的公共衛生問題.為了考察某種流感疫苗的效果，某實驗室隨機抽取100只健康小鼠進行試驗，得到如下列聯表：
感染 | 未感染 | 總計 | |
注射 | 10 | 40 | 50 |
未注射 | 20 | 30 | 50 |
總計 | 30 | 70 | 100 |
參照附表，在犯錯誤的概率最多不超過__________的前提下，可認為“注射疫苗”與“感染流感”有關系．
（參考公式：
.）
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若一個人下半身長（肚臍至足底）與全身長的比近似為
（
，稱為黃金分割比），堪稱“身材完美”，且比值越接近黃金分割比，身材看起來越好，若某人著裝前測得頭頂至肚臍長度為72
，肚臍至足底長度為103，根據以上數據，作為形象設計師的你，對TA的著裝建議是（ ）
A.身材完美，無需改善B.可以戴一頂合適高度的帽子
C.可以穿一雙合適高度的增高鞋D.同時穿戴同樣高度的增高鞋與帽子
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐P﹣ABCD的底面ABCD是正方形，PD⊥平面ABCD，E為PB上的點，且2BE=EP．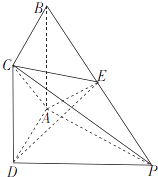 
（1）證明：AC⊥DE；
（2）若PC= 
BC，求二面角E﹣AC﹣P的余弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
