
【題目】市政府為了節約用水,調查了100位居民某年的月均用水量(單位:![]() ),頻數分布如下:
),頻數分布如下:
分組 |
|
|
|
|
|
|
|
|
|
頻數 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |

(1)根據所給數據將頻率分布直圖補充完整(不必說明理由);
(2)根據頻率分布直方圖估計本市居民月均用水量的中位數;
(3)根據頻率分布直方圖估計本市居民月均用水量的平均數(同一組數據由該組區間的中點值作為代表).
【答案】(1)直方圖見解析;(2)2.02;(3)2.02.
【解析】分析:(1)根據表格中數據,求出所缺區間的縱坐標,即可將頻率分布直方圖補充完整;(2)根據直方圖可判斷中位數應在![]() 組內,設中位數為
組內,設中位數為![]() ,則
,則![]() ,解得
,解得![]() ;(3)每個矩形的中點橫坐標與該矩形的縱坐標相乘后求和,即可得到本市居民月均用水量的平均數.
;(3)每個矩形的中點橫坐標與該矩形的縱坐標相乘后求和,即可得到本市居民月均用水量的平均數.
詳解:(1)頻率分布直方圖如圖所示:
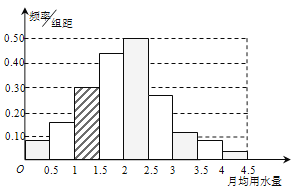
(2)∵0.04+0.08+0.15+0.22=0.49<0.5,
0.04+0.08+0.15+0.22+0.25=0.74>0.5,
∴中位數應在[2,2.5)組內,設中位數為x,
則0.49+(x-2)×0.50=0.5,
解得x=2.02.
故本市居民月均用水量的中位數的估計值為2.02.
(3)0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25
+2.75×0.14+3.25×0.06+3.75×0.04+4.25×0.02
=2.02.
故本市居民月均用水量的平均數的估計值為2.02.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域為[﹣1,1],圖象如圖1所示;函數g(x)的定義域為[﹣2,2],圖象如圖2所示,設函數f(g(x))有m個零點,函數g(f(x))有n個零點,則m+n等于( )
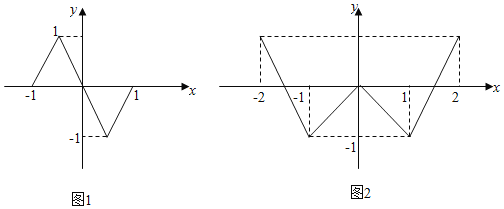
A. 6 B. 10 C. 8 D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中, ![]() 的兩個頂點
的兩個頂點![]() 的坐標分別為
的坐標分別為![]() ,三個內角
,三個內角![]() 滿足
滿足![]() .
.
(1)若頂點![]() 的軌跡為
的軌跡為![]() ,求曲線
,求曲線![]() 的方程;
的方程;
(2)若點![]() 為曲線
為曲線![]() 上的一點,過點
上的一點,過點![]() 作曲線
作曲線![]() 的切線交圓
的切線交圓![]() 于不同的兩點
于不同的兩點![]() (其中
(其中![]() 在
在![]() 的右側),求四邊形
的右側),求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于![]() 的一元二次方程
的一元二次方程![]() ,其中
,其中![]() 。
。
(I)若![]() 隨機選自集合
隨機選自集合![]() ,
,![]() 隨機選自集合
隨機選自集合![]() ,求方程有實根的概率;
,求方程有實根的概率;
(Ⅱ)若![]() 隨機選自區間
隨機選自區間![]() ,
,![]() 隨機選自區間
隨機選自區間![]() ,求方程有實根的概率。
,求方程有實根的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() .
.
(![]() )證明數列
)證明數列![]() 是等比數列,求出數列
是等比數列,求出數列![]() 的通項公式.
的通項公式.
(![]() )設
)設![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() .
.
(![]() )數列
)數列![]() 中是否存在三項,它們可以構成等比數列?若存在,求出一組符合條件的項;若不存在,說明理由.
中是否存在三項,它們可以構成等比數列?若存在,求出一組符合條件的項;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的上下兩個焦點分別為
的上下兩個焦點分別為![]() ,過點
,過點![]() 與
與![]() 軸垂直的直線交橢圓
軸垂直的直線交橢圓![]() 于
于![]() 兩點,
兩點, ![]() 的面積為
的面積為![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知![]() 為坐標原點,直線
為坐標原點,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() 兩個不同的點,若
兩個不同的點,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 所圍成封閉圖形面積為
所圍成封閉圖形面積為![]() ,曲線
,曲線![]() 是以曲線
是以曲線![]() 與坐標軸的交點為頂點的橢圓, 離心率為
與坐標軸的交點為頂點的橢圓, 離心率為![]() . 平面上的動點
. 平面上的動點![]() 為橢圓
為橢圓![]() 外一點,且過
外一點,且過![]() 點
點
引橢圓![]() 的兩條切線互相垂直.
的兩條切線互相垂直.
(1)求曲線![]() 的方程;
的方程;
(2)求動點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com