
【題目】(本題滿分12分)某食品廠為了檢查一條自動包裝流水線的生產情況,隨機抽取該流水線上![]() 件產品作為樣本稱出它們的重量(單位:克),重量的分組區間為
件產品作為樣本稱出它們的重量(單位:克),重量的分組區間為![]() ,
,![]() , ,
, ,![]() ,由此得到樣本的頻率分布直方圖,如圖所示.
,由此得到樣本的頻率分布直方圖,如圖所示.
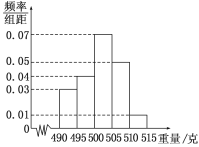
(1)根據頻率分布直方圖,求重量超過![]() 克的產品數量;
克的產品數量;
(2)在上述抽取的![]() 件產品中任取
件產品中任取![]() 件,設
件,設![]() 為重量超過
為重量超過![]() 克的產品數量,求
克的產品數量,求![]() 的分布列;
的分布列;
(3)從該流水線上任取![]() 件產品,求恰有
件產品,求恰有![]() 件產品的重量超過
件產品的重量超過![]() 克的概率.
克的概率.
【答案】(1)![]() (件);
(件);
(2)Y的分布列為
| 0 | 1 | 2 |
P |
|
|
|
(3)![]() .
.
【解析】
試題分析:(1)根據頻率分布直方圖即可求出;(2)求![]() 的分布列;由于
的分布列;由于![]() 為重量超過
為重量超過![]() 克的產品數量,抽取的
克的產品數量,抽取的![]() 件產品中任取
件產品中任取![]() 件,因此
件,因此![]() 的可能取值為0,1,2.由古典概型的概率求法,分別求出概率,即得分布列;(3)從該流水線上任取
的可能取值為0,1,2.由古典概型的概率求法,分別求出概率,即得分布列;(3)從該流水線上任取![]() 件產品,求恰有
件產品,求恰有![]() 件產品的重量超過
件產品的重量超過![]() 克的概率,這符合二項分布,利用二項分布即可求出恰有
克的概率,這符合二項分布,利用二項分布即可求出恰有![]() 件產品的重量超過
件產品的重量超過![]() 克的概率.
克的概率.
試題解析:(1)根據頻率分布直方圖可知,重量超過505克的產品數量為
![]() (件). (/span>2分)
(件). (/span>2分)
(2)![]() 的可能取值為0,1,2. (3分)
的可能取值為0,1,2. (3分)
![]() (4分)
(4分)
![]() (5分)
(5分)
![]() (6分)
(6分)
Y的分布列為
| 0 | 1 | 2 |
P |
|
|
|
(3)利用樣本估計總體,該流水線上產品重量超過505克的概率為0.3 (8分)
令![]() 為任取的5件產品中重量超過505克的產品數量,
為任取的5件產品中重量超過505克的產品數量,
則![]() , (10分)
, (10分)
故所求概率為![]() (12分)
(12分)


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是平行四邊形,∠BCD=135°,側面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分別為BC,AD的中點,點M在線段PD上. 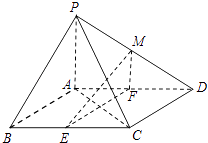
(1)求證:EF⊥平面PAC;
(2)如果直線ME與平面PBC所成的角和直線ME與平面ABCD所成的角相等,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=120°,AC=3,△ABC的面積等于 ![]() ,D為邊長BC上一點.
,D為邊長BC上一點. 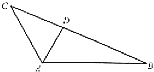
(1)求BC的長;
(2)當AD= ![]() 時,求cos∠CAD的值.
時,求cos∠CAD的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數y=f(x)對任意的x都滿足f(x+1)=﹣f(x),當﹣1≤x<1時,f(x)=x3 , 若函數g(x)=f(x)﹣loga|x|至少6個零點,則a取值范圍是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)
設△ABC三個內角A、B、C所對的邊分別為a,b,c. 已知C=![]() ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如圖,在△ABC的外角∠ACD內取一點P,使得PC=2.過點P分別作直線CA、CD的垂線PM、PN,垂足分別是M、N.設∠PCA=α,求PM+PN的最大值及此時α的取值.


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天氣預報說,未來三天每天下雨的概率都是0.6,用1、2、3、4表示不下雨,用5、6、7、8、9、0表示下雨,利用計算機生成下列20組隨機數,則未來三天恰有兩天下雨的概率大約是 .
757 220 582 092 103 000 181 249 414 993
010 732 680 596 761 835 463 521 186 289.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某客運公司用A,B兩種型號的車輛承擔甲、乙兩地間的長途客運業務,每車每天往返一次.A,B兩種車輛的載客量分別為36人和60人,從甲地去乙地的營運成本分別為1600元/輛和2400元/輛.公司擬組建一個不超過21輛車的客運車隊,并要求B型車不多于A型車7輛.若每天要以不少于900人運完從甲地去乙地的旅客,且使公司從甲地去乙地的營運成本最小,那么應配備A型車、B型車各多少輛?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com