
【題目】已知函數f(x)=![]() .(a>0)
.(a>0)
(1)若a=1,證明:y=f(x)在R上單調遞減;
(2)當a>1時,討論f(x)零點的個數.
【答案】見解析
【解析】(1)證明:當x≥1時,f′(x)=![]() -1≤0,f(x)在[1,+∞)上單調遞減,f(x)≤f(1)=0;
-1≤0,f(x)在[1,+∞)上單調遞減,f(x)≤f(1)=0;
當x<1時,f′(x)=ex-1-1<0,f(x)在(-∞,1)上單調遞減,且此時f(x)>0.
所以y=f(x)在R上單調遞減.
(2)若x≥a,則f′(x)=![]() -a≤
-a≤![]() -a<0(a>1),
-a<0(a>1),
所以此時f(x)單調遞減,令g(a)=f(a)=ln a-a2+1,
則g′(a)=![]() -2a<0,所以f(a)=g(a)<g(1)=0,
-2a<0,所以f(a)=g(a)<g(1)=0,
即f(x)≤f(a)<0,故f(x)在[a,+∞)上無零點.
當x<a時,f′(x)=ex-1+a-2,
①當a>2時,f′(x)>0,f(x)單調遞增,
又f(0)=e-1>0,f![]() <0,所以此時f(x)在
<0,所以此時f(x)在![]() 上有一個零點.
上有一個零點.
②當a=2時,f(x)=ex-1,此時f(x)在(-∞,2)上沒有零點.
③當1<a<2時,令f′(x0)=0,解得x0=ln(2-a)+1<1<a,所以f(x)在(-∞,x0)上單調遞減,在(x0,a)上單調遞增.
f(x0)=e![]() +(a-2)x0=e
+(a-2)x0=e![]() (1-x0)>0,
(1-x0)>0,
所以此時f(x)沒有零點.
綜上,當1<a≤2時,f(x)沒有零點;當a>2時,f(x)有一個零點.


科目:高中數學 來源: 題型:
【題目】【2016年高考四川理數】設函數f(x)=ax2-a-lnx,其中a ∈R.
(Ⅰ)討論f(x)的單調性;
(Ⅱ)確定a的所有可能取值,使得![]() 在區間(1,+∞)內恒成立(e=2.718…為自然對數的底數).
在區間(1,+∞)內恒成立(e=2.718…為自然對數的底數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電視劇《人民的名義》中有一個低矮的接待上訪服務窗口,假設群眾辦理業務所需的時間互相獨立,且都是10分鐘的整數倍,對以往群眾辦理業務所需的時間統計結果如下:
辦理業務所需的時間(分) | 10 | 20 | 30 | 40 | 50 |
頻率 | 0.3 | 0.3 | 0.2 | 0.1 | 0.1 |
假設排隊等待辦理業務的群眾不少于3人,從第一個群眾開始辦理業務時開始計時.
(Ⅰ)估計第三個群眾恰好等待40分鐘開始辦理業務的概率;
(Ⅱ)![]() 表示至第20分鐘末已辦理完業務的群眾人數,求
表示至第20分鐘末已辦理完業務的群眾人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(1),在等腰梯形![]() 中,
中, ![]() ,
, ![]() 是梯形的高,
是梯形的高, ![]() ,
, ![]() ,現將梯形沿
,現將梯形沿![]() ,
, ![]() 折起,使
折起,使![]() 且
且![]() ,得一簡單組合體
,得一簡單組合體![]() 如 圖(2)示,已知
如 圖(2)示,已知![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點.
的中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成的銳二面角大小.
所成的銳二面角大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】社會調查人員希望從對人群的隨機抽樣調查中得到對他們所提問題誠實的回答,但是被采訪者常常不愿意如實做出應答.
1965年Stanley·L.Warner發明了一種應用概率知識來消除這種不愿意情緒的方法.Warner的隨機化應答方法要求人們隨機地回答所提問題中的一個,而不必告訴采訪者回答的是哪個問題,兩個問題中有一個是敏感的或者是令人為難的,另一個是無關緊要的,這樣應答者將樂意如實地回答問題,因為只有他知道自己回答的是哪個問題.
假如在調查運動員服用興奮劑情況的時候,無關緊要的問題是:你的身份證號碼的尾數是奇數嗎;敏感的問題是:你服用過興奮劑嗎.然后要求被調查的運動員擲一枚硬幣,如果出現正面,就回答第一個問題,否則回答第二個問題.
例如我們把這個方法用于200個被調查的運動員,得到56個“是”的回答,請你估計這群運動員中大約有百分之幾的人服用過興奮劑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為公差不為零的等差數列,首項
為公差不為零的等差數列,首項![]() ,
, ![]() 的部分項
的部分項![]() 、
、![]() 、 、
、 、![]() 恰為等比數列,且
恰為等比數列,且![]() ,
,![]() ,
,![]() .
.
(1)求數列![]() 的通項公式
的通項公式![]() (用
(用![]() 表示);
表示);
(2)設數列![]() 的前
的前![]() 項和為
項和為![]() , 求證:
, 求證: ![]() (
(![]() 是正整數
是正整數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校在2011年的自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組:第1組[75,80),第2組[80,85),第3組[85,90),第4組[90,95),第5組[95,100]得到的頻率分布直方圖如圖所示.
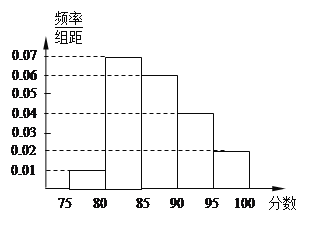
(Ⅰ)分別求第3,4,5組的頻率;
(Ⅱ)若該校決定在筆試成績高的第3,4,5組中用分層抽樣抽取6名學生進入第二輪面試,求第3,4,5組每組各抽取多少名學生進入第二輪面試?
(Ⅲ)在(Ⅱ)的前提下,學校決定在這6名學生中隨機抽取2名學生接受甲考官的面試,求第4組至少有一名學生被甲考官面試的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com