已知函數(shù)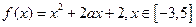
.
（1）當(dāng)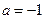
時，求函數(shù)f(x)
的最大值和最小值；
（2）求實數(shù)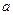
的取值范圍，使
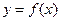在區(qū)間
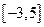上是單調(diào)函數(shù)
科目：高中數(shù)學(xué) 來源： 題型：解答題
函數(shù)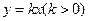
的圖象與函數(shù)
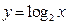的圖象交于兩點
（
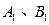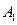在線段
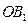上，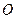
為坐標(biāo)原點），過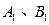作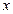
軸的垂線，垂足分別為
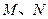，并且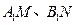
分別交函數(shù)
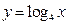的圖象于
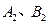兩點．
(1)試探究線段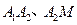
的大小關(guān)系；
(2)若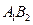
平行于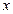軸，求四邊形
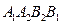的面積．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
（本小題滿分14分） 對于函數(shù)f（x），
若存在x0∈R，使f（x0）=x0成立， 則稱x0為f（x）的不動點. 已知函數(shù)f（x）=ax2+（b+1）x+b－1（a≠0）
（1）當(dāng)a=1，b=－2時，求f（x）的不動點；
（2）若對于任意實數(shù)b，函數(shù)f（x）恒有兩個相異的不動點，求a的取值范圍
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
（本小題滿分14分）一塊邊長為10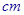
的正方形鐵片按如圖所示的陰影部分裁下,然后用余下的四個全等的等腰三角形加工成一個正四棱錐形容器,試建立容器的容積
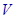與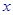
的函數(shù)關(guān)系式,并求出函數(shù)的定義域.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
（本小題12分）某創(chuàng)業(yè)投資公司擬投資開發(fā)某種新
能源產(chǎn)品，估計能獲得x∈[10,1000]萬元的投資收益.現(xiàn)準(zhǔn)備制定一個對科研課題組的獎勵方案：獎金y（單位：萬元）隨投資收益x（單位：萬元）的增加而增加，且獎金不超過9萬元，同時獎金不超過投資收益的20%.
（Ⅰ）若建立函數(shù)f(x)模型制定獎勵方案，試用數(shù)學(xué)語言表述公司對獎勵函數(shù)f(x)模型
的基本要求；
（Ⅱ）現(xiàn)有兩個獎勵函數(shù)模型：(i) y＝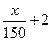
；(ii) y＝4lgx－3.試分析這兩個函數(shù)模型
是否符合公司要求？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
（14
分）某工廠每天生產(chǎn)某種產(chǎn)品最多不超過40件，并且在生產(chǎn)過程中產(chǎn)品的正品率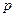
與每日生產(chǎn)產(chǎn)品件數(shù)
(
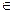
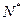)間的關(guān)系為
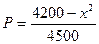，每生產(chǎn)一件正品盈利4000元，每出現(xiàn)一件次品虧損2000元.（注：正品率=產(chǎn)品的正品件數(shù)÷產(chǎn)品總件數(shù)×100%）
（Ⅰ）將日利潤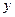
（元）表示成日產(chǎn)量（件）的函數(shù)；
（Ⅱ）求該廠的日產(chǎn)量為多少件時，日利潤最大？并求出日利潤的最大值
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
…………2分
，
； 
………6分
………7分
，即
時，
在
，即
時，
………11分
. ……1
；
.
.
,解方程
;
的取
值范圍
； (2) 