Question

（理科）已知函數＝x²－4x＋a＋3，g(x)＝mx＋5－2m．

(Ⅰ)若y＝f(x)在[－1，1]上存在零點，求實數a的取值范圍；

(Ⅱ)當a＝0時，若對任意的x₁∈[1，4]，總存在x₂∈[1，4]，使f(x₁)＝g(x₂)成立，求實數m的取值范圍；

(Ⅲ)若函數y＝f(x)（x∈[t，4]）的值域為區間D，是否存在常數t，使區間D的長度為7－2t？若存在，求出t的值；若不存在，請說明理由（注：區間[p，q]的長度為q－p）．

 

Answer 1

【答案】

(Ⅰ)：因為函數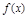＝x²－4x＋a＋3的對稱軸是x＝2，

所以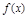在區間[－1，1]上是減函數，

因為函數在區間[－1，1]上存在零點，則必有：

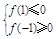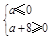即，解得，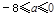

 

故所求實數a的取值范圍為[－8，0] ．

(Ⅱ)若對任意的x₁∈[1，4]，總存在x₂∈[1，4]，使f(x₁)＝g(x₂)成立，只需函數y＝f(x)的值域為函數y＝g(x)的值域的子集．

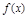＝x²－4x＋3，x∈[1，4]的值域為[－1，3]，下求g(x)＝mx＋5－2m的值域．

①當m＝0時，g(x)＝5－2m為常數，不符合題意舍去；

②當m＞0時，g(x)的值域為[5－m，5＋2m]，要使[－1，3]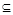 [5－m，5＋2m]，

需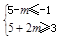，解得m≥6；

 

③當m＜0時，g(x)的值域為[5＋2m，5－m]，要使[－1，3]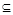 [5＋2m，5－m]，

需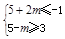，解得m≤－3；

 

綜上，m的取值范圍為．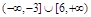

(Ⅲ)由題意知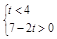，可得．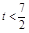

 

①當t≤0時，在區間[t，4]上，f(t)最大，f(2)最小，

所以f(t)－f(2)＝7－2 t即t²－2t－3＝0，解得t＝－1或t＝3（舍去）；

②當0＜t≤2時，在區間[t，4]上，f(4)最大，f(2)最小，

所以f(4)－f(2)＝7－2 t即4＝7－2t，解得t＝；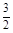

 

③當2＜t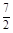＜時，在區間[t，4]上，f(4)最大，f(t)最小，

 

所以f(4)－f(t)＝7－2t即t²－6t＋7＝0，解得t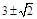＝（舍去）

綜上所述，存在常數t滿足題意，t＝－1或．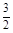

 

【解析】略